LES CANNES À MOUCHE de DANIEL BRÉMOND
| Accueil | Genèse | Structure alvéolaire | Assemblage par épissures | Études de profils | Résultats théoriques | Souvenirs | Contact |

| Accueil | Genèse | Structure alvéolaire | Assemblage par épissures | Études de profils | Résultats théoriques | Souvenirs | Contact |
Dans ce chapitre il sera largement question d’un principe de construction familier aux ingénieurs ou architectes : l’égale contrainte. Si l'on n’est pas dans ce cas, le réflexe est de consulter internet. Or, au moins en français, on ne trouve quasiment rien, c’est pourquoi je crois utile de l’illustrer par trois exemples.
On teste un câble en lui accrochant une charge de masse M. Sa section S a été calculée proportionnellement au poids P (P = Mg) de la charge. Le rapport P/S permet de calculer l’allongement du câble et renseigne sur les risques de rupture. C’est la contrainte à laquelle il est soumis, analogue à une pression (dans ce cas négative) qui s’exprime en N/m² (Newton par mètres carrés). Au cours de l’essai ce câble casse brutalement exactement à la sortie du treuil sur lequel il est enroulé. Pourquoi à cet endroit précis ? Parce que c’est là qu’il sera soumis à la plus grande contrainte du fait de son poids propre qui s’ajoute à P. Pour y remédier, il n’y a pas d’autre moyen que de faire varier sa section de telle façon qu’en tout point elle soit proportionnelle non plus seulement à P mais au total de P et de celui du câble déroulé. Le problème est simple mais la solution l’est moins. La section répond à une loi exponentielle.
Mais le calcul vaut d’être fait ! Ainsi constitué, toutes les fibres du matériau, à n’importe quel niveau, s’allongeront dans les mêmes proportions. C’est un premier exemple d’égale contrainte. Et tout autre profil exigera plus de matière si l’on veut conserver la même marge de sécurité. Si dans la pratique les câbles ont une section constante c’est parce que leur masse est le plus souvent négligeable vis-à-vis de la charge, mais il serait possible de les alléger tout en gardant ces mêmes marges de sécurité. Une structure qui respecte l’égale contrainte du matériau est optimisée.
Après cet exemple en traction, un en compression : un pilier vertical doit soutenir une charge. C’est le même problème à l’envers et si l’on veut respecter le même principe, la section doit être maximum à la base et s’amincir jusqu’à la charge. On a tous en mémoire l’image d’une construction qui respecte ce principe : La Tour Eiffel ! Sa forme n’est pas l’œuvre d’un artiste mais est issue des calculs de deux ingénieurs qui ne lui ont pas donné leur nom : Patrice KOECHLIN formé à l’Institut Polytechnique de Zurich et Émile NOUGIER, « leur préoccupation majeure étant la résistance des matériaux, avant d’aborder l’esthétique ». J’ai aussi trouvé qu’elle était construite « de façon exponentielle ». Si bien qu’il est difficile d’imaginer que l’égale contrainte sous la charge et les forces du vent n’ait pas été le principe de base des calculs. Cette construction sans logements, sans bureaux, en quelque sorte un acte gratuit, m’a fasciné dès l’enfance par sa fonctionnalité. Cette passion n’est pas étrangère à mes recherches sur les cannes à mouche, les plus légères possible. Plus loin, j’évoquerai justement des cannes avec un profil en Tour Eiffel.
Un dernier exemple plus riche dans une situation de flexion. Une plateforme en porte à faux ou mieux un plongeoir, supporte une charge en son extrémité. Sa déformation sera une flexion qui étire les fibres du dessus et tasse celles du dessous, le partage se faisant par rapport à une nappe de fibres non sollicitées dites fibres neutres. Si le matériau, élastique se présente en plaques d’épaisseur constante, le profil d’égale contrainte, si on néglige la masse du tremplin, est un triangle isocèle, parce que sa largeur croît proportionnellement à la distance à l’extrémité comme le moment fléchissant. Mais, comme pour le câble, si la masse propre du matériau n’est pas négligeable, il faudra prévoir un premier renfort. Et si le plongeur l’utilise pour se propulser, les différents tronçons du plongeoir n’étant plus seulement soumis à la pesanteur mais à une accélération croissante depuis la base jusqu’à la pointe, il faudra calculer une nouvelle forme. C’est la méthode que j’ai utilisée dans mes calculs sur les profils de cannes, en sachant que de la variabilité des lancers et des lanceurs fait que l’égale contrainte ne peut être atteinte au sens strict mais qu’il faut s’en approcher.
Que se passe t-il dans le cas contraire ? En général, ça se voit ! S’il y a un vernis, il craquelle à la longue dans les zones soumises aux plus forts allongements qui seront les premières à perdre leurs qualités mécaniques, ce qui fera dire que la canne est usée. Mais cela peut être aussi visible sur la ligne qui se déploie. Si elle ondule, cela trahit des différences entre zones faibles et zones fortes. En effet, les flexions maximales atteintes aux différents niveaux de la canne ne sont pas simultanées mais montent depuis la main jusqu’à la pointe ; quand cette onde de déformation passe dans une zone plus contrainte, sa vitesse est ralentie (exactement, c’est l’accélération de la vitesse de l’onde qui diminue !), ce qui influe sur le mouvement de l’anneau de tête et se traduit par une ondulation de la ligne. Ce défaut peut être plus ou moins corrigé par le lanceur ou en chargeant la canne, le plus difficile étant de réaliser une canne capable de lancer une soie plus légère que celle prévue, sans qu’elle ondule.
Le critère d’égale contrainte qui privilégie le bon usage du matériau reste une approche parmi d’autres. Si au contraire on s’intéresse au lanceur il serait logique de rechercher les profils qui assurent le meilleur rendement, défini comme rapport entre l’énergie fournie à la soie et celle fournie par le lanceur RS/RL ? J’ai choisi la première approche, mais comme l’égale contrainte minimise les sections il ne serait pas étonnant que les deux méthodes convergent. Bonne lecture de la suite. Daniel BRÉMOND - 23 mars 2021

Force est de constater, et mon expérience couvre plusieurs décennies, une amélioration des cannes à mouches. Elles sont plus légères, elles permettent de lancer plus loin, et surtout elles demandent moins d’énergie au lanceur, elles fatiguent moins. A ce sujet, le bon test c’est de faire des faux lancers avec une longueur donnée de soie, par exemple 10 à 12 m. C’est surprenant comme la crampe musculaire arrive vite. Et ce d’autant plus que la canne est plus…SOUPLE ! Oui, la souplesse fatigue ! Les flexions, augmentées sur une canne souple, absorbent de l’énergie. C’est comme pour un pneu, un matelas, ou une semelle: Plus ils sont souples « pour plus de confort » plus ils consomment de carburant ou épuisent nos muscles ! À ce sujet une digression sur la qualité des soies : ceux qui ont eu la chance d’utiliser des soies naturelles ont pu juger « qu’elles fonctionnaient bien », sans pour autant réaliser pourquoi. On a parlé de densité supérieure... ? La raison n’est pas là. Prenez une soie naturelle et un échantillon de soies synthétiques et tirez dessus. Vous constaterez que la soie naturelle ne s’allonge pratiquement pas comparée à la moyenne des soies synthétiques. Et plus les soies s’allongent au cours du lancer pendant lesquels elles sont soumises à de fortes tractions, plus elles absorbent d’énergie, cette part étant soustraite à celle que vous avez produite pour les propulser. Si vous hésitez entre deux soies, tirez dessus et choisissez celle qui s’allonge le moins !
Mais revenons à l’amélioration des cannes.
Elle est à mettre au compte, pour une bonne part, de nouveaux matériaux. Ainsi, les fibres de verre ont été surclassées et abandonnées. Mais le choix de la longueur, de la distribution des épaisseurs, ce qu’on appelle le profil, a aussi joué un rôle essentiel. En particulier pour le merveilleux matériau qu’est le bambou refendu.
Sur 50 ans d’observation, les cannes en bambou se sont raccourcies, allégées, un progrès auquel a contribué pour les constructions amateurs la « structure alvéolaire », et ont gagné en puissance, expression vague qui signifie qu’on peut communiquer plus d’accélération à la soie grâce à une augmentation bien distribuée des épaisseurs.
Cette évolution s’est faite essentiellement de façon empirique, selon le principe « essais / résultats » et très minoritairement par « calculs / résultats ». J’expliquerai pourquoi j’ai choisi la deuxième démarche.
La première se conçoit si on dispose d’une méthode de taillage qui permette de modifier facilement les profils. Mais même sur une courte longueur, moins de 3 m, avec des épaisseurs déjà expérimentées, en particulier au point clef où le lanceur communique l’énergie qui va propulser la soie c'est-à-dire dans la poignée, les possibilités de variations sont immenses et les réussites rares. Telles les dernières cannes de l’autrichien Walter BRUNNER qui utilisait une machine rudimentaire comparée à celle de Pezon & Michel. Les baguettes circulaient sur une table mobile, la conicité était donnée par une came qui la relevait. Modifier cette came était l’affaire de quelques coups de lime. En faisant équipe avec le très bon lanceur Hans GEBETSROITHER, Walter BRUNNER a mis au point des cannes de plus en plus courtes, de plus en plus puissantes, vraiment très efficaces. Je possède une « Gebetsroither » 2,12 m pour soie N°6 qui est remarquable.
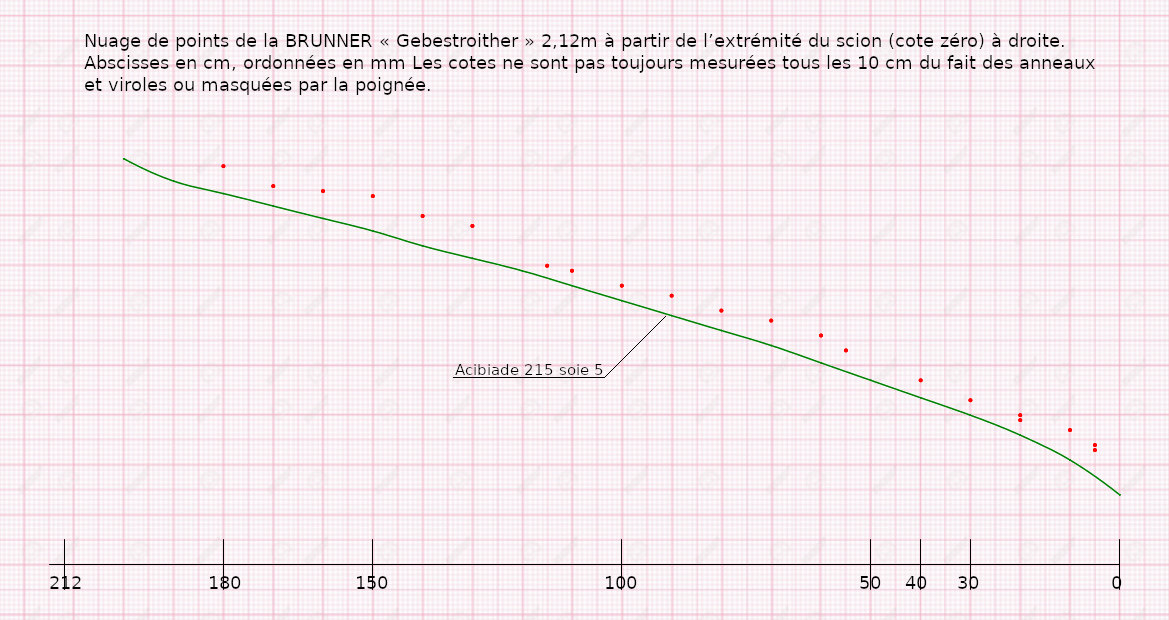
Voici son profil, mesuré sur le vernis.
Profil “ Gebestroither ” depuis le talon. La canne mesure 2,12 m. La poignée 23 cm. Je donne les cotes sur plats à 0,1 mm près, une meilleure précision n’ayant pas beaucoup de sens quand les mesures sont faites sur le vernis. J’ai fait figurer les cas où, suivant les trois directions possibles des mesures, la dispersion atteint 0,1 mm. On constate une forte conicité en sortie de poignée puis une très faible jusqu’à la virole. Comme elle est livrée avec deux scions, j’ai mesuré les deux sans trouver de différences significatives. On peut constater qu’il n’est pas facile de relier les points par un tracé « moyen ». Il n’en demeure pas moins que cette canne est vraiment très efficace pour catapulter une soie N°6 à la condition de pratiquer la double traction.
| 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | Virole | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | 210 |
| P | P | P | 8,2 8,1 |
7,7 | 7,5 | 7,4 7,3 |
7 | 6,9 6,8 |
5,9 5,8 |
5,6 | 5,5 | 5,2 | 4,9 | 4,6 | 4,25 | 3,8 | 3,2 | 3 | 2,7 | 2,4 2,3 |
Comme je préconise de représenter les profils depuis l’anneau de tête, voici le nuage de points de la canne de Walter BRUNNER avec, pour comparer, le profil d’une de mes cannes “ Alcibiade ” de longueur proche : 2,15 m mais qui est strictement prévue pour soie N°5.
| cm | 212 | 200 | 190 | 180 | 170 | 160 | 150 | 140 | 130 | 115 | 110 | 100 | 90 | 80 | 70 | 60 | 55 | 40 | 30 | 20 | 10 | 5 | 0 |
| mm | x | x | x | 8 | 7,6 | 7,5 | 7,4 | 7 | 6,8 | 6 | 5,9 | 5,6 | 5,4 | 5,1 | 4,9 | 4,6 | 4,3 | 3,7 | 3,3 | 3 2,9 |
2,7 | 2,4 2,3 |
x |
| cm | 215 | 200 | 190 | 180 | 170 | 160 | 150 | 140 | 130 | 110 | 110 | 100 | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 | 0 |
| mm | x | 8,15 | 7,7 | 7,45 | 7,2 | 6,95 | 6,7 | 6,4 | 6,15 | 5,9 | 5,6 | 5,3 | 5,0 | 4,7 | 4,4 | 4,05 | 3,7 | 3,35 | 3,0 | 2,6 | 2,1 | 1,4 |
J’ai essayé plus court, je crois une « Cheri » de 1,80 m pour soie N°5. Même satisfaction ! Merci de me permettre une nouvelle digression : Hans GEBETSROITHER et Aimé DEVAUX avaient la même corpulence. Ce dernier utilisait une canne en fibre de verre du célèbre magasin « Le coin de pêche » tenu par Sacha TOLSTOÏ. Aimé DEVAUX lançait en force, sur la truite. J’ai toujours pensé que son posé direct provoquait un mouvement réflexe, comme le geste machinal de chasser une mouche sur notre bras alors que ce n’est qu’une brindille qui nous a effleuré, en l’occurrence pour la truite un réflexe de prédation déclenchant le gobage. Je suis certain qu’Aimé DEVAUX aurait apprécié les cannes de Walter BRUNNER.
Je déconseille les plus courtes à ceux qui ne maîtrisent pas la double traction. Pour ma part je la pratique à toutes distances, sans forcer, le travail de ma main droite (je suis gaucher pour la pêche ou le tennis) soulageant la canne au lieu de la charger.
J’ai expliqué dans « de A à Z » combien la rencontre de Walter BRUNNER m’avait été profitable, m’incitant à maîtriser la totalité de la fabrication en partant des troncs de bambou bruts. Il avait exprimé un avis mitigé sur la structure alvéolaire, m’expliquant qu’il avait suffisamment de cannes à réparer et ne souhaitait pas se compliquer la vie !
C’est à Yves RAMEAUX, déjà à l’origine de mes recherches sur l’assemblage en biseau, que je dois de l’avoir rencontré. Yves RAMEAUX m’avait donné rendez vous à Munich pour me faire découvrir quelques uns des merveilleux parcours du célèbre « Club du refendu » dont il était actionnaire. Quels souvenirs ! Des truites et ombres passant le kilo ! Et nous en avions ramenés, après les avoir plongés dans de l’air liquide, grâce à son ami JPM qui menait des recherches sur les éphémères à la faculté de Munich ! Une journée avait été consacrée à rendre visite à Walter BRUNNER. Yves RAMEAUX qui avait aussi la passion de la photographie avait apprécié ses clichés d'odonates[1]Note [1] – Ordre d'Insectes hémimétaboles, terrestres à l'état adulte, aquatiques à l'état larvaire, connus sous le nom de Libellules ou Demoiselles., mais l’essentiel avait porté sur la construction des cannes, Yves RAMEAUX servant de traducteur.
Est-ce de la voix de Walter BRUNNER ou de celle de Tim BEDFORD, un autre artisan dont je reparlerai plus loin, que j’ai entendu pour la première fois les termes de « Waves action » et « One pièce action » ? Les deux qualificatifs méritent d’être expliqués.
Voilà qui nous change des heureuses formules, sur le plan publicitaire au moins, inventées par Charles RITZ telle : l’action parabolique ! ...qui ne se rapportent qu’à la courbure de la canne, et encore !
Une citation à ce sujet, assez claire même non traduite[2]Note [2] – Pour les non-anglophones : « Charles Ritz s'est rendu compte plus tard du potentiel marketing de l'expression "action parabolique" dans son livre "A Fly Fisher’s Life" (édition de 1972) : "...C'est cette action que j'ai appelée "Parabolique", bien que ce ne soit qu'une expression car la courbure de la canne n'a absolument rien a voir avec une parabole." Cette expression n'apparaît pas dans la version française originelle de ce livre (1953)... ». : « Charles Ritz later recognized the marketing potential of the phrase “parabolic action” in his book A Fly Fisher’s Life (1972) : “... This is the action which I have called “Parabolic,” though the term is only a figure of speech, and the curve of the rod has absolutely nothing to do with a parabola.” This sentence does not appear in the original French version of this book (1953)[3]Note [3] – Intitulée « Pris sur le vif », cette première version a été publiée en 1953 aux éditions Librairie des Champs Élysées, Paris.... »
Dans les deux expressions anglo-saxonnes, c’est la sensation ressentie par le lanceur et le mouvement de la canne qui sont évoquées. Je m’étonne quelles ne soient pas plus utilisées en France.
Qu’est ce qu’une « wave action » ? Cela concerne les cannes avec un profil en « Tour Eiffel » avec une forte conicité en sortie de poignée, et peu prononcée sur le scion. Il en découle une très forte courbure de la canne au cours du lancer, et la sensation d’une vague (d’où wave !) ou d’une onde de déformation qui se propage sans transition, le scion se comportant déjà comme un gros fil, jusqu’à la soie. Pensez à une cravache prolongée ! Ce n’est pas mon choix mais ce n’est pas désagréable du tout ! La boucle de soie est très serrée et elle se déploie bas sur l’eau du fait de la forte courbure de la canne. Pas plus haut avec une « wave action » de 8 pieds 2 pouces soit 2,50 m qu’avec une 1,80 m de W. BRUNNER ! Inconvénients : fatigue rapide, pas moyen de modifier la trajectoire si besoin, il faut suivre le mouvement plus que le diriger, ferrer avec le bras et non avec le poignet sinon l’anneau de tête se déplace à contre sens. Mais ça marche et certains lanceurs sont plus à l’aise avec ce type de canne qu’avec celles de BRUNNER ou les miennes, en particulier tous ceux, et ils sont nombreux, qui peinent à attendre le plein déploiement de la soie avant de la propulser dans l’autre sens. Du fait de la faiblesse du scion, avec les « wave action », il est justement nécessaire d’anticiper pour bander le ressort de la canne.
Et les « One pièce action » ? Quand j’ai construit l’ISO 80, 2,20 m, 80 g, comme déjà dit en introduction, j’ai été surpris par l’impression de disposer d’un grand bras de levier et surtout de ressentir nettement la force exercée par l’anneau de tête sur la soie. Cette première canne et toutes les suivantes construites selon ma méthode de calcul pour approcher de l’égale contrainte, se rattachent au type « One pièce action » qui peut dérouter un lanceur habitué à faire travailler la canne : elles plient peu. J’ai retrouvé ce type d’action sur certaines cannes en fibre de carbone.
J’ai développé cette question dans deux articles : « De A à Z » et « Cannes longues, cannes hautes ».
Dans le premier (visible ici), pour éviter les anglicismes j’ai utilisé les termes « cannes propulsives » et « cannes impulsives ». Dans le second (non visible sur le site) je distinguais la longueur de la canne et la hauteur à laquelle la soie se déploie. Il est bien évident qu’en dépit de leur longueur, les cannes « wave action » ou « propulsives » ne tiennent pas plus haut la soie que les « one pièce action » ou « impulsives », même pour un écart de taille allant jusqu’à soixante centimètres.

Nous avons vu que la résistance à la flexion était proportionnelle à la puissance 4 du diamètre de la section (ou cote sur plats pour un hexagone). Ce n’est pas une situation courante. Si on double les dimensions d’un terrain son aire est multipliée par 4. Pour une cuve, son volume est multiplié par 8, pour une canne sa raideur est multipliée par 16 ! Pour cette raison, ce qu’on voit et peut mesurer, c'est-à-dire l’épaisseur, dissimule d’une certaine façon la grandeur physique qui intervient réellement, en l’occurrence la raideur ou résistance à la flexion \(R\) (qui est le produit du moment quadratique de la section \(Q\) par le module de Young \(Y\). Voir le chapitre « Résultats théoriques »)
Malheureusement, il est difficile sinon impossible de représenter sur un papier millimétré la variation de raideur d’une canne de la pointe du scion au talon, ce qui est pourtant sa caractéristique principale car c'est là que se cache l'action de la canne. Un exemple suffit pour le comprendre : imaginons que le diamètre varie de 1,6 mm en pointe à 8 mm au talon, donc dans la proportion de 1 à 5. Dans ce cas la raideur variera de 1 à 625 (625 = 5⁴) et il n’y a pas d’échelle qui permette de visualiser une telle amplitude (l’usage d’une graduation semi logarithmique ne résout pas le problème car le graphique modifié masque d’une certaine façon la réalité physique).
Voici la méthode que je propose :
Voilà ce que j’obtiens pour les talons de trois cannes dont les cotes ont été publiées dans les deux versions de « La canne à mouche » de Josselin de LESPINAY :
la “ Standard ”, “ Alcibiade ” et “ Bourrasque ”. Je trouve les schémas très « expressifs » ! Ils prouvent combien une modeste modification des épaisseurs produit une très forte modification de la raideur. À vous de juger !
18 avril 2020
Courbes C⁴ / 500 des talons de trois de mes cannes et de leurs profils
repérés dans l'ordre de leur sortie :
N° 1 “ Standard ” - N° 2 “ Alcibiade ” - N° 3 “ Bourrasque ”
On constatera l'amplification des augmentations de raideur par rapport à celles des épaisseurs : une augmentation de 20 % de l'épaisseur du talon de la “ Standard ” fait plus que doubler la raideur dans le bas du talon de “ Bourrasque ” !

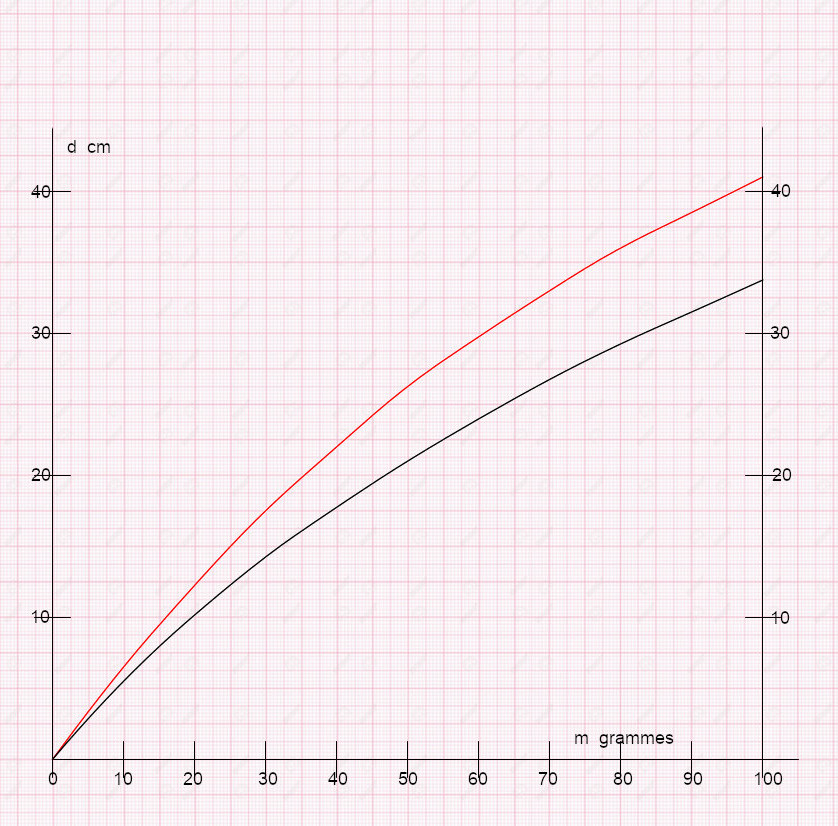
Distances à l'anneau de tête
Comparaison de deux cannes en bambou refendu de 2,50 m de long, pour soies N° 5
Modèle Ritz de Pezon et Michel - 120 g
Ardente N° 61 construite en 1981 - 103 g - Structure alvéolaire - Assemblage par épissure
(ce n'est pas un profil calculé)


Comme pour la structure alvéolaire et le dessin rationnel des assemblages en biseaux, je précise les rencontres qui ont favorisé mes recherches.
Celle de l’américain Tim BEDFORD qui, après avoir pris sa retraite, avait racheté l’atelier (machine et stock de bambous) de DICKERSON. Il avait donc fait ses débuts de constructeur au moment où d’autres préfèrent aller à la pêche. Sa passion l’a conduit deux fois en France, la première fois, en compagnie de son épouse, pour s’informer des techniques des constructeurs européens. Ils étaient passé me voir à Champagnole et je les avais retrouvés le lendemain à Amboise pour une visite chez Pezon et Michel fructueuse et sympathique malgré leur fatigue : mes chers amis n’ayant pas trouvé d’hôtel avaient passé la nuit dans leur voiture ! Leur prochaine étape était Hardy en GB. La deuxième fois Tim était seul, invité par Yves RAMEAUX dans sa maison près de Champagnole. Il nous avait fait un exposé sur ses constructions. Le lendemain nous étions allé pêcher dans l’Ain ; Tim fabriquait et utilisait des cannes « Waves action ».
Celle de mon collègue à Champagnole B. D. professeur de mécanique qui a construit mes meilleures règles pour tailler les profils, puis la machine permettant d’usiner les ébauches des baguettes triangulaires qui est en photo dans « De A à Z ». Elle est actuellement équipée d’un nouvel outil avec quatre jeux de pastilles carbure au lieu de deux. Également trois cales ingénieuses pour les mesures (voir « Mesure avec une cale triangulaire »). Encore à son actif un dispositif astucieux composé d’un moteur de rôtisseuse avec un tube en acier fixé sur son axe, suffisamment épais pour le munir de trois vis à 180° constituant ainsi un mandrin rudimentaire. Le tout sur un support assez lourd avec une fixation permettant de varier « l’angle de tir », l’objet ayant l’allure d’un obusier miniature ! Dans quel but ? Faire tourner lentement un scion ou un talon fixé dans le mandrin, pour le vernir « à la goutte », selon la méthode que j’ai expliquée à Josselin de LESPINAY.
Une nouveauté technique m’a aussi été favorable : c’est un modèle resté célèbre de calculatrice, la HP 41 sans laquelle je n’aurais pas pu écrire mes programmes de calculs des profils.
Deux certitudes au départ de mes recherches : qu’il n’était pas concevable d’avoir un saut des diamètres au niveau de la virole mais surtout qu’un talon et un scion avec des conicités constantes ne pouvait pas être la bonne solution, qu’il fallait des pentes variables, ce que les anglo-saxons appellent « compound taper » (ainsi la canne “Syrinx” construite pour Albert DRACHKOVITCH, voir photos) et ce, dans le but de remédier à des défauts manifestes. Par exemple j’avais observé, sur de nombreuses cannes, que leur courbure atteignait son maximum entre les deux derniers serpentiformes, prouvant qu’il y avait là une sous épaisseur car elle devrait s’accentuer entre le dernier serpentiforme et l’anneau de tête (voir le schéma précédent « Comparaison de deux cannes de 2,50 m »). Également, sur des cannes anciennes, j’avais constaté qu’après une longue durée d’utilisation, leur vernis se craquelait en sortie de poignée et dans la même partie du scion. Des craquelures exactement perpendiculaires à l’axe de la canne révélant un étirement de la pellicule de vernis, supérieur dans ces zones à celui des zones voisines. C’était la preuve qu’il en était de même pour les fibres de bambou soumises à une plus forte contrainte[4]Note [4] – Je rappelle que la contrainte est proportionnelle à l’allongement relatif des fibres (cf. « Résultats théoriques ») dans ces zones.. D’où l’idée de rechercher des profils de cannes s’approchant le mieux possible de l’égale contrainte.
Ce n’est pas une vue de l’esprit, c’est une démarche générale pour les structures soumises à des déformations. C’est d’autant plus important quand elles sont soumises à des mouvements rapides. Une surépaisseur c’est une masse en plus à mouvoir qui « fatigue » les zones en sous épaisseur.
Comment y parvenir et est-ce possible d’y parvenir ? Sans aucun doute ! Et déjà d’une façon purement expérimentale. Les motoristes par exemple, pour dessiner des bielles, des vilebrequins sans points faibles ni lourdeurs inutiles utilisent des « jauges de contraintes » ou « jauge extensométrique, instrument destiné à mesurer les variations dimensionnelles d'un élément de structure dans le but d'évaluer les contraintes qu'il subit. »
Ces jauges sont basées sur la variation de résistivité de conducteurs disposés sur la pièce à étudier. Bien difficile à mettre en œuvre pour une canne à mouche ! Mais il existait une méthode plus rustique qui m’a été expliquée il y a bien longtemps, lors d’une visite aux bureaux d’étude des usines BERLIET à Bourg-en-Bresse, au moment où justement je me penchais sur les calculs de profil. Elle consiste à recouvrir les pièces d’un vernis “craquelant”. Après essais, la direction et l’espacement des craquelures renseignent sur les contraintes subies par les fibres extérieures. Ces vernis n’ont rien à voir avec les produits pour vieillir les tableaux ou autres effets décoratifs. Cette technique, qui a même été utilisée dans l’aviation, semble plus ou moins obsolète, supplantée en particulier par des méthodes optiques (lumière polarisée), mais les renseignements ne manquent pas, tant dans les sites en français qu’anglo-saxons : Voir « Brittle lacker, cracking varnish stress analysis » ; ils seraient à base de colophane ? Comment les utiliser : en les étalant partiellement sur la canne, en pratiquant suffisamment de lancers à des distances variables pour faire apparaître les craquelures et en déduire suivant leur concentrations les zones à renforcer. Bien entendu, il s’agit d’une méthode statistique, les contraintes maximum dépendant de la longueur et de la cadence des lancers, du style du lanceur. Mais n’en est-il pas de même pour un vilebrequin soumis à des contraintes variables suivant le régime du moteur ?
On retiendra donc la possibilité de s’approcher expérimentalement d’un profil d’égale contrainte.
Mais, ne disposant pas comme Walter BRUNNER des moyens de procéder à de multiples essais, c’est par le calcul que j’ai tenté de le faire. Le but étant choisi, la mise au point d’une méthode de calcul, d’abord avec l’aide de graphiques puis informatisée, le réglage des outils pour respecter les cotes, et la réalisation d’un prototype ont représenté une succession de tâches laborieuses. Mais quelle bonne surprise à la fin ! Le prototype, ma canne N° 35 “ ISO 80 ” (ISO pour égale contrainte, 80 g, rebaptisée Balerne du nom d’un petit affluent de l’Ain en aval de Champagnole) achevée à la fin des années 1970, s’est révélée différente de toutes celles que j’avais pu essayer. Ce fut une expérience autrement gratifiante que le tâtonnement, au sens propre jubilatoire !
Jusqu’à ce jour j’avais renoncé à diffuser mes méthodes, mes programmes. Pas pour la raison invoquée par Josselin de LESPINAY dans la 2e édition de « La canne à mouche » : « Si Daniel BRÉMOND ne souhaitait pas voir sa méthode de calcul publiée, c’est parce qu’il savait qu’en partant de ses calculs, on pouvait faire de mauvaises cannes, puisqu’il suffit de rentrer des données (par exemple : canne de 4 m pour soie de 3), le programme vous sortira un profil mathématiquement cohérent mais absurde en tant que canne à pêche. » mais du fait simplement de la difficulté à les expliquer.
Par contre il a tout à fait raison concernant mes programmes qui ne contiennent pas encore des limites ou des consignes précises pour les choix des paramètres. Ce sera expliqué plus loin.
L’âge venant j’ai jugé bon de combler cette lacune.
Malheureusement, malgré tous mes efforts, la difficulté retombe sur le lecteur ! Mes calculs sont laborieux à suivre mais au moins ils sont publics, peuvent être vérifiés et discutés. Je peux aussi répondre à des questions, mon adresse mail figure au chapitre « Contact ».

1) Mes calculs ne visent qu’à répartir les épaisseurs entre la cote sur plats sous la main, qui résulte d’un choix et celle en pointe qui doit être la plus faible possible mais capable de supporter une autre contrainte que le moment fléchissant : l’effort tranchant. D’après mon expérience il me semble imprudent de descendre en dessous de 1,4 mm. De même, la longueur de la canne résulte elle aussi d’un choix et non d’un calcul.
2) Ma prise en compte des contraintes qui vont provoquer la courbure de la canne utilise comme modélisation une tige droite qui pivote autour d’un axe fixe ! Je suis bien conscient, depuis que j’ai mis au point mes programmes de calcul au début des années 80, que cette hypothèse simplificatrice est discutable pour une canne à mouche alors qu’elle serait légitime pour des objets qui se déforment peu, par exemple des clubs de golf. C’est une des raisons pour lesquelles mes méthodes ont évolué.
Dans le dernier paragraphe je proposerai une technique originale, expérimentale mais étayée par des calculs théoriques, d’amélioration de mes profils calculés. Je l’ai mise au point en cette année 2020.

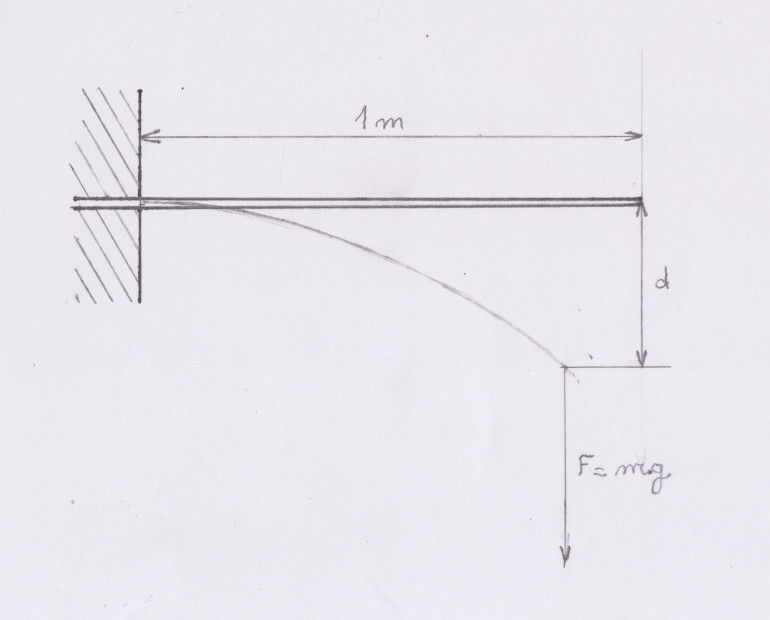
Elle m’a fait simplement retrouver un résultat bien connu d’égale contrainte pour une poutre soumise à une force unique à son extrémité. Le moment fléchissant étant proportionnel à la longueur du bras de levier, donc à la distance depuis l’anneau de tête, \(MtF = k \times L\), la condition d’égale contrainte vue dans « Résultats théoriques » : \(c= \large \sqrt[3] {\frac{MtF} {cte}}\)équivaut à \(c=k \sqrt[3] {L}\)
Ce que l'on peut formuler par : les épaisseurs croissent proportionnellement à la racine cubique de la distance à l’anneau de tête.
Le fait d'imposer une valeur de la cote sur plat en un point de la canne permet de calculer la valeur de \(k\), puis de calculer point par point toutes les autres.
En respectant cette relation on obtient bien des vrais profils d’égale contrainte, mais à la condition d’être dans une situation statique, comme soutenir un poisson hors de l’eau ou tendre le fil pour décrocher une mouche ; elle n’est donc pas à retenir si on veut améliorer le comportement de la canne au cours des lancers.
Exemple de profil d’égale contrainte sans tenir compte de la masse du bambou avec une longueur depuis la main (point \(O\) de la canne) de 200 cm et une cote sur plats en \(O\) de 8 mm.

Autres exemples en faisant varier le coefficient de proportionnalité :
Famille de profils \(c = k \sqrt[3] {l}\)
si \(l = 0 \;\) \(c =\)1,4 ou 1,5 mm
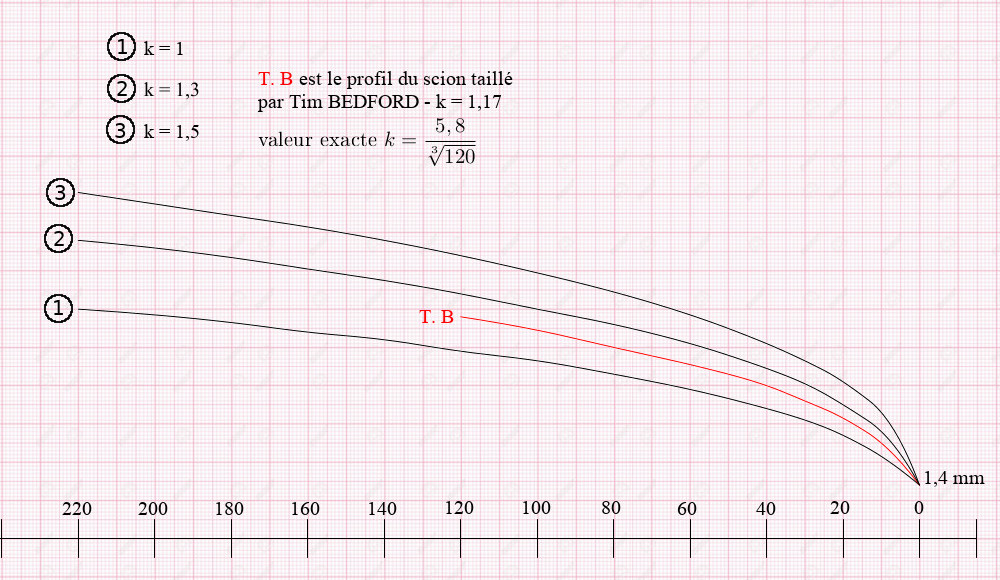
C’est ce type de profil que j’avais soumis à Tim BEDFORD ! Il m’avait envoyé peu de temps après des baguettes pour un talon avec une pente de 2,5/1000 et des baguettes, au nombre de huit, deux en plus sans doute en cas d’accident, avec ce 1er profil calculé \(c=1,17 \sqrt[3] {L}\).
J’ai « alvéolé » et collé les baguettes du talon, ce qui m’a permis de juger de l’exceptionnelle qualité du bambou. Quant aux huit baguettes du scion elles sont toujours en attente, précieusement conservées en pensant avec émotion à ce cher ami.
Pourquoi ? Motivé par ce contact amical au-delà de l’Atlantique, j’avais réalisé que je ne pouvais pas en rester à cette première approximation. La canne doit propulser la soie mais aussi “ s’auto-propulser ”. C’est ce qui apparaît lors d’un mouvement de lancer à vide, sans soie : la canne se courbe du fait de sa propre inertie. Il me fallait tenir compte de cette nécessité “ d’auto-propulsion ”. De ce fait, il n’était pas question de gâcher les précieuses baguettes pour vérifier une idée déjà périmée.

Mes méthodes de calculs qui ont suivi cette première tentative conservent le but d’approcher de l’égale contrainte mais tiennent compte des moments de flexion dus à la propulsion de la canne par elle-même en plus de celui dû à la soie.
Un exemple en m’aidant d’un graphique.
Il s’agit de calculer le profil d’une canne dont la longueur depuis la main jusqu’à l’anneau de tête est 200 cm. La cote sur plats sous la main est 8 mm (Point \(O\) de la canne) et la masse moyenne de soie manœuvrée 12 g (ce qui correspond à peu près à un posé à 15 m). Le profil sera référencé par P 200-8-12
Le préalable est de définir un profil fictif \(P_0\) qui va permettre d’évaluer les masses de bambou. Par exemple, un profil conique, de 8 mm sous la main à 2 mm en pointe, pente 3/1000. Les répétions de calculs, (itérations) prouveront que les cotes calculées convergent au sens mathématique du terme et sont indépendantes de \(P_0\). Plus tard, dans le programme de calcul en fin de chapitre, cette stabilisation des résultats est évaluée par la ligne delta.

La canne est partagée en tronçons de 10 cm de long assimilés à des « morceaux de crayon » sans conicité, dont le centre de gravité est le milieu de la longueur. La cote sur plat \(C\) permettant de calculer le volume de l’élément est la cote au centre de gravité.
On a \(V= C^2 \times \displaystyle \frac {\sqrt {3}} {20} \;\) \( \underline {C \text { étant exprimée en mm}}\)
La masse volumique du bambou alvéolaire, avec vernis, anneaux est estimée à 1g/cm². Elle est donc exprimée par le même nombre que \(V\).
Pour les deux premières données signalées en bleu qui concernent la géométrie de la canne, je donnerai une méthode radicale qui supprime toute approximation. Concernant la masse volumique du bambou, alvéolaire ou pas, une donnée plus précise aura un effet négligeable sur la répartition entre les moments de flexions dus à la propulsion de la soie (exactement à son accélération) et ceux dus à la propulsion de la canne elle-même. Cette précision apportée n'aurait pas plus d'effet qu'une modification légère de la masse de la soie, inférieure à 0,5 g. La seule amélioration réelle est, dans le cas d’un assemblage par virole, de tenir compte du moment dû à sa propulsion.
Le moment de flexion dû à la soie en \(O\) est égal à \(M_s \times {\large \gamma} \times L\)
Dans l’exemple L = 200 cm, \(\large \gamma \) est un paramètre.
Pour une commodité de représentation j’ai choisi de diviser cette valeur par \(L \times \large \gamma\). Ce qui fait que le moment qui s’exprime en Nm (Newton mètre) ou joules par radian, n’est plus représenté que par la masse de la soie, dans l’exemple 12 g (échelle 1cm/g). Mais je respecterai les proportions en faisant de même pour les moments fléchissants \(M_i\) dus à la propulsion des tronçons de la canne qui seront donc, eux aussi, représentés en grammes. Et ce sont ces valeurs en grammes que je totaliserai graphiquement. Les cotes sur plats seront calculées point par point, proportionnellement à la racine cubique de leur total. Je reviendrai sur cette question car sans cette division par \(L \times \large \gamma\), dont le seul but est de faciliter la construction graphique, une explication plus rationnelle est possible, se rattachant au moment d’inertie de l’ensemble canne - soie.
Si \(\large \gamma_i\) est l'accélération à laquelle est soumis le centre de gravité d’un tronçon, \(\large \gamma_i = \large \gamma \times \frac{OG_i} {L}\)
Cette distance à \(O\) du centre de gravité d’une section correspond à la ligne « position CG » du tableau.
Si \(m_i\) est la masse de la section numéro \(i\) , et \(M_i\) le moment créé à la base, on a \(M_i = m_i \times {\large \gamma \times \frac{OG_i} {L}} \times OG_i\)
Pour respecter les proportions par rapport au moment de la soie, il faut diviser ce nombre par \( {\large \gamma} L\) .On obtient :
Représentation de \(M_i = m_i \times \large \gamma \times \frac{OG_i} {L} \times \frac{OG_i}{\gamma L}\)
Représentation de \(M_i = m_i \times \left( \large \frac{OG_i} {L} \right) ^2\)
Puisque \(\large \frac {X_i} {L}\) est sans dimension, la représentation des moments s’exprime bien en grammes.
| Numéro des sections | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Position CG cm | 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 | 105 | 115 | 125 | 135 | 145 | 155 | 165 | 175 | 185 | 195 |
| Cote au CG mm | 7,85 | 7,55 | 7,25 | 6,95 | 6,65 | 6,35 | 6,05 | 5,75 | 5,45 | 5,15 | 4,85 | 4,55 | 4,25 | 3,95 | 3,65 | 3,35 | 3,05 | 2,75 | 2,45 | 2,15 |
| Indice de position | 0,025 | 0,075 | 0,125 | 0,175 | 0,225 | 0,275 | 0,325 | 0,375 | 0,425 | 0,475 | 0,525 | 0,575 | 0,625 | 0,675 | 0,725 | 0,775 | 0,825 | 0,875 | 0,925 | 0,975 |
| Indice \(\large \gamma\) | 0,025 | 0,075 | 0,125 | 0,175 | 0,225 | 0,275 | 0,325 | 0,375 | 0,425 | 0,475 | 0,525 | 0,575 | 0,625 | 0,675 | 0,725 | 0,775 | 0,825 | 0,875 | 0,925 | 0,975 |
| Masses section en g | 5,34 | 4,94 | 4,55 | 4,18 | 3,82 | 3,49 | 3,17 | 2,86 | 2,57 | 2,30 | 2,037 | 1,793 | 1,564 | 1,351 | 1,154 | 0,972 | 0,806 | 0,655 | 0,520 | 0,400 |
| Moment à la base | 0,0033 | 0,028 | 0,071 | 0,128 | 0,194 | 0,264 | 0,335 | 0,403 | 0,465 | 0,518 | 0,561 | 0,593 | 0,611 | 0,616 | 0,606 | 0,584 | 0,548 | 0,501 | 0,445 | 0,381 |
| Moments cumulés à la base | 7,85 | 7,85 | 7,82 | 7,75 | 7,62 | 7,43 | 7,17 | 6,83 | 6,43 | 5,96 | 5,45 | 4,9 | 4,3 | 3,68 | 3,06 | 2,46 | 1,88 | 1,32 | 0,82 | 0,381 |
Somme graphique des moments de flexion.
Chaque moment additionnel dû à la propulsion de la canne par elle-même prend naissance au centre de gravité d’une section, d’où le graphique suivant dans lequel les ordonnées des points de la courbe supérieure donnent la somme des moments fléchissants dus à la propulsion de la soie et des tronçons de la canne en tous ses points.
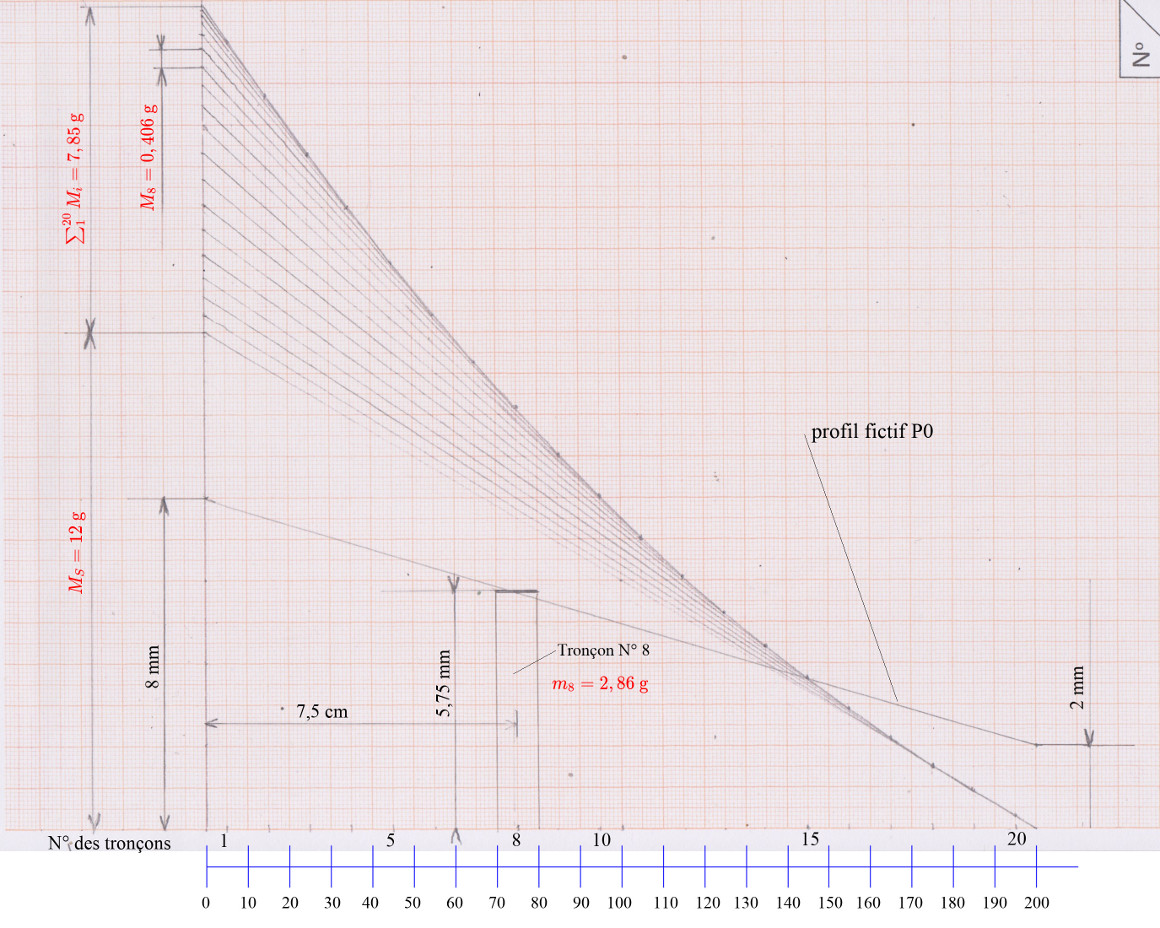
On relève en \(O\), sur ce schéma et sur le tableau \(M_s + \sum_{1}^{20} m_i \left( \dfrac{OG_i}{L} \right) = 12 + \textbf{7,85} = 19,85 \; \text {g}\)
La valeur de 7,85 g est une sorte d’“ effective tip mass ” de la canne qui va augmenter quand on remplacera \(P_0\) par \(P_1\) dans le calcul des masses des tronçons (\( P_1\) est plus “ogival” que \(P_0\)). Prenons 8 g comme valeur approchée ce qui fera 20 g pour l’ensemble Canne / Soie.
On remarquera que dans le moment exercé par le lanceur pour accélérer l’ensemble Canne / Soie, 40 % sera consacré à la canne et 60 % à la soie !
Calcul de \(k\) avec \(C_0 = 8 \; \text {mm}\)
\(8 = k \sqrt[3] {19,75}\) \(k = {\large \frac {8} {\sqrt[3] {19,75}}} = 2,960\)
Calculs des cotes sur plats point par point : On relève sur le graphique la somme des moments tous les 10 cm.
Puis \(Cx = 2,960 \sqrt [3] {Mx} \;\)Par exemple : \(C_{90} = 2,960 \sqrt [3] {8,5} = 6,04 \; \text {mm}\)
| x = position | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| Moment | 19,85 | 18,5 | 17 | 15,6 | 14,3 | 13 | 11,85 | 10,7 | 9,6 | 8,5 | 7,5 | 6,5 | 5,6 | 4,75 | 4 | 3,25 | 2,5 | 1,8 | 1,2 | 0,6 | 0 |
| \(C_1(x)\) | 8,00 | 7,83 | 7,6 | 7,4 | 7,185 | 6,96 | 6,75 | 6,52 | 6,3 | 6,04 | 5,79 | 5,52 | 5,26 | 4,98 | 4,7 | 4,38 | 4,0 | 3,6 | 3,14 | 2,5 | 1,4 |
Méthode de calcul des moments cumulés en un point X de la canne.
Indépendamment de la lecture sur le graphique de la somme des moments dus à la propulsion de la soie et de la canne, un exemple de calcul :
Somme des moments additionnels dus à la canne en X à 1m de O.
Cela concerne les sections de 11 à 20 de la canne.
On retrouve les résultats extraits du tableau complet dans les lignes 2, 3 et 5. Seul change l’indice de position qui exprimait le rapport entre la distance \(OG_i/L\) remplacé par \(XG_i/L\) (qui correspond à un changement de « bras de levier »)
La ligne 7 donne les moments partiels en \(X\) et la 8 leur cumul en \(X\).
| Numéro des sections | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Position CG cm | 105 | 115 | 125 | 135 | 145 | 155 | 165 | 175 | 185 | 195 |
| Cote au CG mm | 4,85 | 4,55 | 4,25 | 3,95 | 3,65 | 3,35 | 3,05 | 2,75 | 2,45 | 2,15 |
| Indice de position | 0,025 | 0,075 | 0,125 | 0,175 | 0,225 | 0,275 | 0,325 | 0,375 | 0,425 | 0,475 |
| Indice \(\large \gamma\) | 0,525 | 0,575 | 0,625 | 0,675 | 0,725 | 0,775 | 0,825 | 0,875 | 0,925 | 0,975 |
| Masses section en g | 2,037 | 1,793 | 1,564 | 1,351 | 1,154 | 0,972 | 0,806 | 0,655 | 0,520 | 0,400 |
| Moment en X | 0,027 | 0,077 | 0,122 | 0,160 | 0,188 | 0,207 | 0,216 | 0,203 | 0,204 | 0,176 |
| Moment cumulés en X = 100 | 1,58 | 1,553 | 1,476 | 1,354 | 1,194 | 1,006 | 0,799 | 0,583 | 0,38 | 0,176 |
En \(X\), le moment de la soie est \(6 \; \text{g} \; \large {\left ( \frac {12 \times 100} {200} \right )} \), celui des 10 tronçons en amont de canne 1,58 g. On a donc une somme de 7,58 g alors qu'elle a été évaluée sur le graphique à 7,57 g.
\(C_1 (100)\) est la valeur calculée. \(C_1 (100) = 2,963 \sqrt [3]{1,58 + 6} = 5,8145 \; \text {mm} \) à la place du 5,7 mm obtenu à partir d'une construction graphique.
Dans le schéma ci-dessous, j’ai représenté et \(C_1\) et \(C_3\) en utilisant le programme de calcul. \(C_3\) est stable !
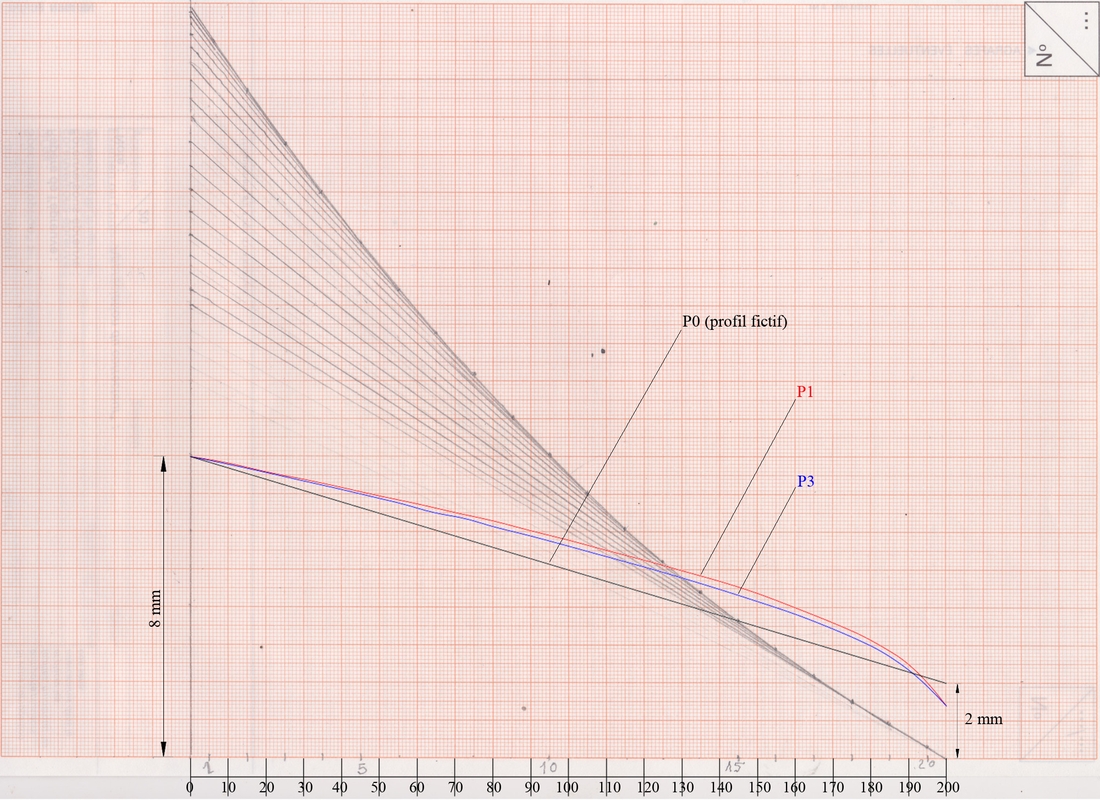
La répartition des épaisseurs entre propulsion de la soie et autopropulsion de la canne.
Pour bien comprendre la différence entre mon approche “ ”primitive » de l’égale contrainte, qui ne tenait pas compte de la masse de bambou qui doit s’autopropulser, puis ma méthode mise au point en 1986 qui en tient compte, il est intéressant de faire apparaître les épaisseurs qui servent à propulser la ligne seule. Par exemple pour P1 puisqu’on connaît la valeur de \(k\) \( \left( k = 2,960 \right)\). Je calcule les cotes grâce à la relation \(C_x = 2,960 \sqrt[3]{Mx}\) mais en remplaçant le moment total dû à la soie et à la canne par le seul moment dû à la soie (voir l’avant dernier tableau). J’appelle ces cotes \(C_Px\), P comme primitif !
| Position | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| Mt soie | 12 | 11,4 | 10,8 | 10,2 | 9,6 | 9,0 | 8,4 | 7,8 | 7,2 | 6,6 | 6,0 | 5,4 | 4,8 | 4,2 | 3,6 | 3,0 | 2,4 | 1,8 | 1,2 | 0,6 | 0 |
| \(C_px\) | 6,78 | 6,67 | 6,54 | 6,4 | 6,3 | 6,15 | 6,0 | 5,9 | 5,7 | 5,55 | 5,4 | 5,2 | 5,0 | 4,8 | 4,55 | 4,25 | 4,0 | 3,6 | 3,15 | 2,5 | 1,4 |
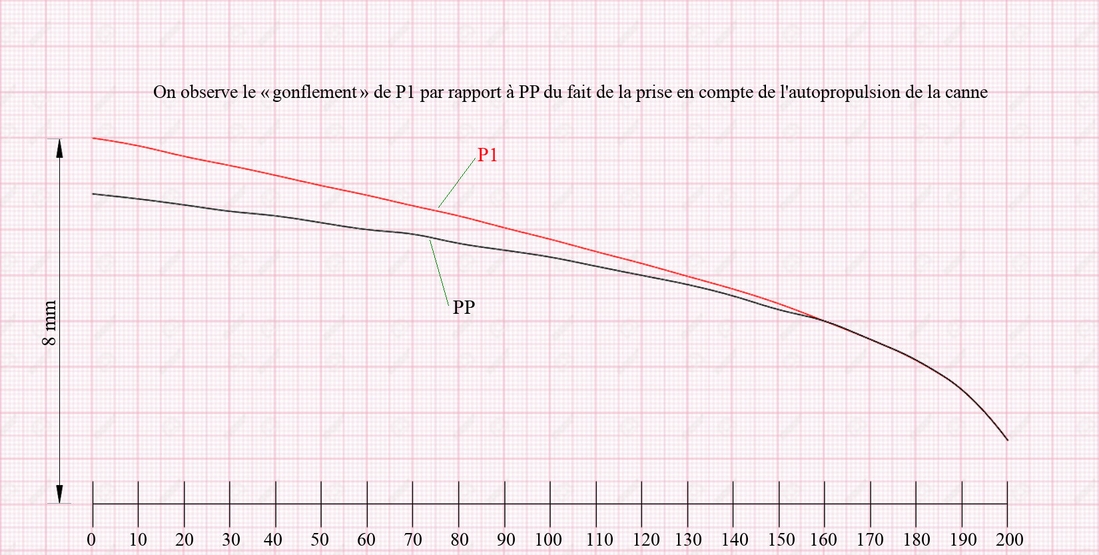
En conclusion mes profils actuels sont de la famille \(c = k \sqrt[3]{l}\) mais augmentés pour tenir compte de l’inertie propre de la canne.
J’ai expliqué plus haut qu’il y avait un moyen pour lever toutes les réserves concernant la modélisation de la canne assimilée à 20 tronçons de 10 cm de long, de diamètre constant égal au diamètre moyen. Les objections : le vrai volume du tronçon n’est pas le même, et le centre de gravité du tronçon n’est pas en son milieu ! C’est vrai, il est décalé vers la base.
On verra ce qu’il en est de leur validité. Le problème est facilement résolu en passant
de \({\Large\sum}_{1}^{20} m_i \left( \displaystyle\frac {OG_i}{L}\right) ^2\)
à \(\displaystyle{\large\int}_0^{200} \rho S_x \times \left( {\large \frac {x}{L}}\right)^2 dx\) où \(\rho S_x dx = dm \)
Un peu de calcul : \(C_x\) est la cote sur plats au point d’abscisse \(x\) donnée par le profil fictif \(P_0\) :
\(C_x = 0,8-0,003 \;x\) en cm[5]Note [5] – Attention, ce coefficient 0,003 n’est qu’un cas particulier. D’une façon générale cette “ pente ” du profil fictif est égale à la différence entre le diamètre à la base et celui à la pointe, divisée par la longueur de la canne.
\(S_x\) est la section de la canne au même point :
\(S_x = {\large \frac {1}{2}} \sqrt{3} \; (0,8-0,003 \; x)^2\) en cm²
\(dV_x\) le volume élémentaire au même point \(dV_x = {\large\frac {1}{2}} \sqrt{3} \; (0,8-0,003 \; x)^2 dx\)
En conservant la masse volumique de 1 g/cm3, la masse élémentaire est donnée par le même nombre en g
Il suffit d’intégrer : \(\displaystyle{\large \int}_0^{200} \displaystyle\frac{\sqrt{3}}{2}\; (0,8-0,003 \; x)^2 \times \left(\displaystyle\frac{x}{L}\right)^2 dx\)
Le résultat est 7,852 en accord (voir tableau ci-dessus) avec celui trouvé avec la modélisation proposée.
Le détail des calculs est visible en cliquant ici
De même pour la somme des moments en un point quelconque de la canne. Je reprends l’exemple de \(X\) à 1 m de \(O\) avec une intégration :
On remplace \(I_x = \displaystyle\sum_{11}^{20} m_i \times \displaystyle\frac {OG_i}{L}\times \displaystyle\frac{XG_i}{L}\)
par \(I_x = \displaystyle\frac{\sqrt{3}}{2} \displaystyle{\large\int}_{100}^{200} (0,8-0,003 \; x)^2 \times \displaystyle\frac {x-100}{200} \times \displaystyle\frac {x}{200}dx\)
Il est plus commode de calculer cette intégrale après un changement de variable, \(x\) désignant la position par rapport à \(X\) et non par rapport à \(O\).
\(I_x = \displaystyle \frac{\sqrt{3}}{2} \displaystyle{\large\int}_{0}^{100} (0,5-0,003 \; x)^2 \times \displaystyle\frac {x}{200} \times \displaystyle\frac {x+100}{200} \times dx\)
0,5 étant le valeur de \(C_x\) en \(X\)
Je ne détaille pas les calculs, le résultat exact est 1,501 à 10⁻⁴ gramme près.
On a donc une somme sur le graphique dépassant 1,5 g , par l’addition des tronçons de 11 à 20, \(I_x\) = 1,58 g et par un calcul intégral, la valeur exacte à 10⁻⁴ g près \(I_x\) = 1,501 g ce qui prouve la cohérence des méthodes.
Mais pourquoi ne pas utiliser depuis le début cette meilleure méthode qu’est l’intégration ?
Parce qu’elle nécessite de connaître la fonction qui définit la cote en tout point, ce qui est réalisé pour le profil \(P_0\) mais pas pour \(P_1\) résultat de la première itération. \(P_1\) est défini par points. Alors trois solutions :
19 mai 2020
J’ai évoqué précédemment une explication plus rationnelle de mes méthodes de calcul se rattachant au moment d’inertie de l’ensemble canne-soie.
Pour cela il faut revenir à la modélisation initiale avec toutes les réserves qu’elle suscite et sur lesquelles je reviendrai.
La canne est assimilée à une tige qui pivote autour du point fixe \(O\) (milieu de la main) et la soie à une masse ponctuelle à une distance \(L\) de \(O\)
L’action d’un moment exercé par la main du lanceur en \(O\) va provoquer une accélération en rotation \( \large \theta "\) de l’ensemble canne-soie. D’après le principe d’action mutuelle le moment résistant de cet ensemble est \(\overrightarrow{-M}\) . Le module \(M\) des ces deux vecteurs opposés est le moment de flexion de la canne en \(O\), en \(N.m\)
Pour un mouvement de translation, on a la relation bien connue :
\( \mathbf{F = m} \large \boldsymbol{\gamma}\) où la masse en kg est la grandeur qui s’oppose à la mise en mouvement.
La grandeur qui s’oppose à la mise en rotation est le moment d’inertie de l’ensemble que je note \(I_{SB}\), S pour soie et B pour bambou \(I_{SB} = I_S + I_B\)
\( \mathbf{M = I_{SB} \boldsymbol{\times \large \theta}"}\)
L’unité de moment d’inertie est le kg.m². Pour des nombres plus parlants, j’utilise le g.cm²
1g.cm² = 10-7 kg.m²
Calcul de \(I_{SB}\)
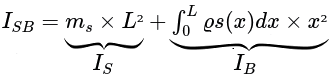
où \(m_s\) est la masse de la soie
\( \rho\) la masse volumique en g/cm³
Calcul du moment de flexion \(M(x)\) en un point quelconque d’abscisse \(x\)
\(M(x) = \left[ ms \times L(L-x) + \displaystyle{\large\int}_{x}^{L} \rho s(x)dx \times x² \right] \times \theta "\)
Suivant la proposition « deux grandeurs proportionnelles à une même troisième sont proportionnelles entre elles », la condition d’égale contrainte :
Le diamètre (ou cote sur plats) est proportionnel à la racine cubique du moment de flexion, équivaut à :
Le diamètre (ou cote sur plats) est proportionnel à la racine cubique du moment d’inertie de l’ensemble canne-soie.
27 mai 2020

Ils nécessitaient des choix comme je l’ai expliqué dans les « notes préalables » :
Ces trois données définissant le profil, exemple P 200 8 12
Le profil \(P_0\) permettant d’amorcer le programme était un profil conique variant de \(C0\) à la base à 2 mm en pointe.
Les calculs des cotes sur plats étaient rigoureusement calqués sur la méthode graphique, avec découpage de la longueur en tronçons de 10 cm.
J’arrêtais les calculs à la 3e itération, les variations des résultats dans les itérations suivantes passant en dessous de 2 centièmes de mm. (On dit que les calculs convergent).
Concernant le profil fictif \(P_0\) un autre choix plausible ne modifiait pas le résultat.
J’ai cherché à améliorer cette première version, en adoptant une autre modélisation du mouvement de la canne. Au lieu d’une rotation de centre \(O\), je l’ai assimilée à une rotation autour d’un point fictif, \(O’\) plus bas que \(O\) (voir schéma). C’est une approche pour tenir compte du mouvement de la main qui doit accompagner celui de la canne. Pourquoi ne pas aller jusqu’à \(OO’ = L\) ? J’y reviendrai dans la partie consacrée au programme F 2020.
Une autre idée basée sur des photos stroboscopiques de ma ” Standard ” montrant une onde de déformation montant de la poignée à l’anneau de tête (voir schéma) m’avait incité à considérer que chaque point \(X\) de la canne était successivement axe de rotation, donc à calculer le moment d’inertie \(I_X\) de la partie amont de la canne et de la ligne par rapport à ce point \(X\). C’était mon programme ” Onde ”. La condition d’égale contrainte dans cette hypothèse était la proportionnalité de la cote sur plats \(C_X\) avec la racine cubique de \(I_X\).
Je n’ai pas observé de différence notable dans les cotes finales avec cette nouvelle méthode que je ne développerai pas.
Compte tenu de la quantité de recherches menées aux US sur les “ fly rods ”, il y a fort à parier que cette idée a déjà été émise et que je ne fais qu’enfoncer une porte ouverte. Mais c’est le lot de toute recherche menée en solitaire ” dans son jardin ”. Une graine qu’on y découvre a pu déjà germer ailleurs !
Quel bilan tirer sur la cinquantaine de cannes aux profils calculés selon ces méthodes ?
Aux impressions que j’ai déjà expliquées, ressenties lors des essais de l’ISO 80, j’ajoute la sensation d’une canne comme débarrassée de poids morts, sans points faibles, répondant dans l’instant à toutes les sollicitations de la main du lanceur. Sans aucun doute mes cannes se rattachent aux « One pièce action » (voir le paragraphe « Wave action, One pièce action » en tête de ce chapitre). Les photos visibles sur le site montrent aussi que mes cannes plient très peu, ce qui rend plus acceptable ma modélisation qui les assimile à des tiges rigides !
Un effet immédiatement sensible de mes méthodes de calcul a été le renforcement du scion. Il est intéressant de remarquer que Charles RITZ avec ses derniers modèles qu’il qualifiait, avec son sens de la formule (qui fait mouche !) de « HS HL[6]Note [6] – Hight Speed Hight Level ce qui veut dire que la canne est suffisamment ferme sur toute sa longueur pour accélérer vigoureusement la soie (HS) qui se déploie du même fait à une bonne hauteur (HL) car sa flexion est limitée. » en refendu puis en fibre de verre, est arrivé par expérience au même résultat mais avec des diamètres en pointe énormes ! Il en est de même pour le tandem Walter BRUNNER - Hans GEBETSROÏTHER. La différence c’est que mes calculs imposent aussi une très forte conicité des pointes de scion, ce qui les rend particulièrement légères. Leur faible inertie (voir aussi « Anneaux de tête ») autorise des mouvements très rapides indispensables pour les lancers très courts, qui peuvent mêmes êtres réduits au bas de ligne.

À ce sujet, un des défauts des cannes en matériaux synthétiques, inhérent à leur mode de fabrication par l’enroulement d’une nappe de fibres sur un mandrin, c’est de ne pouvoir accentuer nettement la conicité en pointe. Un fabricant européen dont j’ai oublié le nom avait résolu le problème en greffant au bout du scion creux, une pointe pleine d’une quinzaine de centimètres de long. C’était disgracieux, comme si la pointe avait été brisée et réparée par un amateur alors que c’était un modèle commercialisé mais, comme j’ai pu m’en rendre compte sur la Loue, elle était très efficace. Une idée pragmatique qui n’a pas eu de succès mais à retenir.
Avec maintenant beaucoup de recul, et en comparant la “ Standard ” et sa version améliorée “ Bourrasque ” (tout au moins à mon sens et pour une majorité d’utilisateurs), il m’apparaît que mes méthodes de calcul sont efficaces dans les parties de la canne où l’énergie est communiquée au bambou par le bambou. C'est-à-dire sur au moins les trois quarts de sa longueur ; mais que la zone où la main transmet l’énergie à la canne peut être utilement renforcée.
On obtiendrait donc un profil avec une très forte conicité en pointe, une zone médiane avec une pente voisine de 0,2 % et, dans le bas du talon, de nouveau une pente augmentée. Ce qu’on peut appeler un S-Profil. Le problème étant de quantifier ce renfort.
Et là, de nouveau, deux méthodes sont possibles : ou procéder à une multitude d’essais ou perfectionner les méthodes de calcul, par exemple en étudiant la vitesse de propagation du flux d’énergie qui monte depuis sa source, la main du lanceur ?
C’est une troisième voie que je propose dans le dernier paragraphe du présent chapitre « 9) Mise au point expérimentale d’un renfort du talon... » avec une méthode surprenante permettant de disposer d’un talon réglable.
On a donc au départ recours à l’empirisme, essais/résultats, mais accompagné des outils mathématiques permettant de quantifier le bon choix. Le prototype “ MBI ” est en cours d’essais.


Téléchargez « F 2020 » (Tableur) ici![]()
Contrairement à mes programmes anciens “ Profil ” et “ Onde ”, dans lesquels la canne est partagée en tronçons de 10 cm, dans le programme « F 2020 » elle est partagée en 25 tronçons égaux quelle que soit la longueur de la canne. Exemples : pour \(L\) = 200 cm, chaque tronçon mesure 8 cm, pour \(L\) = 225 cm, 9 cm et c’est seulement pour \(L\) = 250 cm qu’on retrouve l’écart standard de 10 cm.
Ce n’est pas très commode pour des longueurs telles que 210 cm ou 260 cm ! Cela oblige à tracer le profil pour retrouver les cotes tous les 10 cm mais il existe aussi des programmes qui étaient au départ prévus pour passer des mesures anglo-saxonnes aux mesures métriques et permettent de résoudre ce problème. En voici un, créé par Jean-Claude LEBRAUD (à télécharger ici), qui m’a été transmis par mon ami Serge BODEAU. En dernière colonne figurent les demi cotes sur plats pour régler le gabarit de taillage.
Dans l'onglet « Feuille de saisie » de F 2020, les paramètres à choisir apparaissent en orange colonne B. En écrivant une valeur dans une cellule, elle remplace la précédente.
| Paramètres | Unités | Colonne B |
| \(L\) : longueur de la canne depuis la main (point \(O\)) | cm | cellule B2 |
| \(C_0\) : diamètre ou cote sur plats en \(O\) | cm | cellule B3 |
| \(m_s\) : masse moyenne de soie | gramme | cellule B6 |
La cellule B4 se rapporte au profil fictif \(P_0\) qui permet de commencer les itérations. La valeur zéro a un côté irréel. Mais le choix d’une valeur plus plausible entre 0 et 0,2 cm n’influe pas sur le résultat final. Pourquoi pas 0,14 cm comme sur mes cannes ?
Cellules B7 et B8 : Les valeurs choisies dans les cellules B7 et B8 se rapportent à la modélisation du mouvement de la canne. Elles définissent la proportion entre l’accélération en pointe de scion (cellule B7) et celle de la base de la canne, sous la main du lanceur, notée pour cela « gamma initial » (cellule B8) Il est évident que la valeur en B8 doit être inférieure à celle en B7 et, comme c’est une proportion qui est définie par ces valeurs, je recommande de choisir 1 en B7 et une valeur inférieure à 1 en B8 : \(0 \leq\) gamma initial \(\lt 1\)
Si on impose 0 en B8, la modélisation du mouvement de la canne est une rotation autour du point \(O\) (le poignet ne fait que pivoter sans se déplacer). C’est le choix que j’avais fait pour mon modèle « Standard » que j’ai repris dans l’exemple de profil calculé plus haut. Je suis d’accord avec toutes les réserves que suscitent cette modélisation !
Un moyen de l’améliorer consiste à imposer en B8 une valeur non nulle. Ce qui revient à modéliser le mouvement de la canne par une rotation autour d’un point virtuel \(O’\) plus bas que \(O\). C’est ce qui se produit par exemple si on laisse le poignet fixe et que l’ensemble canne/avant-bras pivote autour du coude. Ce cas particulier sert d’exemple dans la pièce jointe « méthodes pour trouver le "gamma initial" ».
D’une façon générale, plus la canne est courte plus il est nécessaire d’accélérer le bas de la canne. Voir à ce titre ce petit film où tout mon bras se déploie ! La valeur 0,5 en B8 me paraît être la valeur maximum. C’est dans ce cas que \(OO’= L\).
Au-delà, on négligerait la rotation imposée par le poignet. Par exemple si on allait jusqu’à la valeur 1 cela imposerait l’égalité entre l’accélération de la main avec celle de la pointe de scion. Ce qui reviendrait à assimiler le mouvement de la canne à une translation : elle ne ferait qu’avancer ou reculer sans pivoter !
L’effet d’augmenter la valeur de gamma initial majore les moments additionnels dus à l’autopropulsion de la canne par rapport au moment dû à la propulsion de la soie : à diamètre ou cote sur plats constants, la conicité augmente en sortie de poignée donc la canne est plus mince. C’est vérifié dans le tableau ci-dessous pour quatre couples de valeurs (B7 ; B8).
Attention : alors que dans F 2020 les cotes sont en centimètre, je les ai volontairement mises en millimètre pour faciliter la lecture.
Je recommande également de ne pas dépasser 0,5 en B8.
| abscisses | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 | 168 | 176 | 184 | 192 | 200 |
| (1 ; 0) | 8,00 | 7,84 | 7,68 | 7,51 | 7,34 | 7,17 | 7,00 | 6,82 | 6,64 | 6,46 | 6,28 | 6,09 | 5,90 | 5,71 | 5,51 | 5,31 | 5,11 | 4,90 | 4,68 | 4,45 | 4,20 | 3,92 | 3,61 | 3,17 | 2,33 | 1,40 |
| (1 ; 0,25) | 8,00 | 7,82 | 7,64 | 7,49 | 7,28 | 7,01 | 6,91 | 6,73 | 6,54 | 6,35 | 6,16 | 5,97 | 5,78 | 5,59 | 5,39 | 5,19 | 4,99 | 4,78 | 4,56 | 4,33 | 4,09 | 3,82 | 3,50 | 3,07 | 2,27 | 1,40 |
| (1 ; 0,50) | 8,00 | 7,80 | 7,61 | 7,41 | 7,22 | 7,03 | 6,83 | 6,64 | 6,45 | 6,26 | 6,07 | 5,87 | 5,68 | 5,49 | 5,29 | 5,09 | 4,89 | 4,68 | 4,46 | 4,23 | 3,99 | 3,72 | 3,41 | 2,99 | 2,21 | 1,40 |
| (1 ; 0,75) | 8,00 | 7,79 | 7,58 | 7,37 | 7,17 | 6,97 | 6,77 | 6,57 | 6,37 | 6,18 | 5,98 | 5,79 | 5,59 | 5,40 | 5,20 | 5,00 | 4,80 | 4,59 | 4,38 | 4,15 | 3,91 | 3,64 | 3,33 | 2,92 | 2,16 | 1,40 |
On constate de faibles variations des cotes. Toutefois il ne faut pas perdre de vue que dans ce cas, la résistance à la flexion varie dans des proportions quatre fois plus grandes.
Il reste que les modélisations que j’ai utilisées, mêmes améliorées, restent bien en deçà de la complexité des mouvements réels au cours des lancers ce qui laisse le champ libre à leur amélioration, la finalité restant de s’approcher le mieux possible de l’égale contrainte des fibres tout au long de la canne.
C’est une modélisation que j’ai évoquée dans mes programmes sur HP 41 (Voir le schéma qui explique où se place \(O'\) et calcul de \(OO'\) ci-dessous, ainsi que le paragraphe 10 sur E. GARRISSON en fin de chapitre).
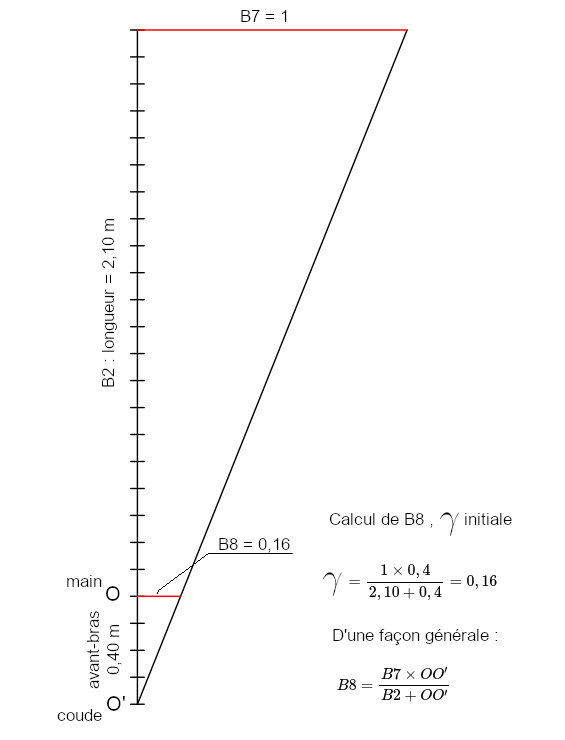
Inversement, si on impose la valeur entrée en B8 (accélération initiale, au niveau de la main) :
\(\scriptsize\dfrac{OO'}{B8}=\dfrac{OO'+L}{B7}\)
\(\scriptsize OO'\times B7=OO'\times B8+L\times B8\)
\(\scriptsize OO'(B7-B8)=L\times B8\)
\(\scriptsize OO'=\dfrac{L\times B8}{B7-B8}\)
Si B7 = 1 (comme recommandé) :
\(\scriptsize OO'=\dfrac{L\times B8}{1-B8}\)
si B8 = 0,5OO' = L
si B8 = 0,75OO' = 3L
Comme expliqué dans le texte, cette dernière valeur en B8 n’est pas un bon choix car elle minimise les effets de la rotation du poignet. C’est pourquoi je préconise de choisir en B8 des valeurs comprises entre 0 et 0,5.
Remarque : les valeurs de OO’ peuvent aussi s’obtenir par un tracé.
Utilisation du programme F 2020 pour d’autres matériaux.
Le programme n’est pas attaché aux seules cannes en bambou. On peut l’utiliser pour des cannes de 3 m en carbone à condition d’évaluer correctement la densité, plus exactement la masse volumique en g/cm³ de l’élément creux, donc de ne pas utiliser la valeur 1,8 g/cm³ de la fibre de carbone !

« ...un renforcement léger du talon supprime généralement le contre-mouvement de la pointe de scion, l'adéquation des cotes de certains profils éprouvés, tels que ceux de Daniel BRÉMOND, assure une propulsion parfaite de la soie et une précision extraordinaire de l'outil. »
Vincent LAFARGE in « Plaidoyer pour le refendu » sur le site « Le vieux moucheur », chapitre « Le bambou refendu »
L’expérience sur plusieurs de mes cannes de l’augmentation de la conicité du bas du talon, sur une longueur de 50 à 60 cm, ce que j’appelle un S-Profil, s’est montrée profitable. Mes profils “ Bourrasque ” et “ Alcibiade ” sont jugés plus performants et agréables que mon profil “ Standard ”. La canne est plus dynamique, elle répond plus vite, sa fréquence de vibration à vide est nettement augmentée, et, curieusement, elle semble plus souple alors qu’elle a été épaissie. Est-ce parce qu’on peut lui communiquer une impulsion plus énergique ?
Mais, en l’absence d’un programme de calcul qui prenne en compte rationnellement le rôle particulier du bas du talon, là où le lanceur apporte l’énergie qui se propagera le long de la canne jusqu’à la soie, comment mettre au point ce renfort sans de multiples essais exigeant chacun de construire un talon ? Et à l’aveugle !
Voilà la méthode expérimentale que je suis en train de tester qui permet de réaliser les essais avec un seul talon, le renfort étant réglable !
Sur ce talon “ M.B.I. ” collé, mais sans poignée, j’ai complété sur 40 cm depuis la zone « sous la main », la section hexagonale par trois baguettes triangulaires de mêmes épaisseurs que celles de l’hexagone, collées fibres dures sur fibres dures à 2h, 6h et 10h, (possible aussi 4h, 8h, 12h) de façon à reconstituer une section en triangle équilatéral. Je l’avais fait pour la première fois sur “ Anaïs ” en 1984, plus pour des raisons esthétiques que mécaniques. L’idée avait été appréciée et reprise.
La nouveauté c’est la longueur des baguettes et le fait que j’ai quantifié leur effet.
La section en triangle équilatéral est 2,7 fois plus rigide que l’hexagone !! C’est dû aux propriétés de cette section que j’ai expliquées dans le paragraphe « Sections polygonales » des « Résultats théoriques ». Si j’ose dire « on en a sous le pied » ! Cela correspondrait à une multiplication de la cote sur plats par 1,28 (racine quatrième de 2,7), par exemple de passer d’une cote sur plats de 8 mm à 11,24 mm ! Et simplement en ajoutant trois baguettes de plus sur les six de l’hexagone ! J’ai pesé mes baguettes avant collage : 12 g. Donc avec 12 g en plus on peut multiplier par 2,7 la raideur de la section hexagonale sur 40 cm de long ! Ça vaut le coup !
Ensuite, il faut évidemment réduire ces renforts. Et là, essais et calculs entrent en jeu pour le dégradé de leur hauteur, sachant qu’il n’est pas obligatoire de garder des triangles complets sous la main mais qu’il faut impérativement finir à zéro au bout du renforcement. Je dis tout de suite qu’une pente régulière n’est pas la bonne solution.
Si \(c\) est la cote sur plats de l’hexagone, si \(e\) est l’épaisseur conservée du renfort triangulaire et \(I(c,e)\) le moment d’inertie ou moment quadratique de la section renforcée par rapport à un axe passant par son centre de gravité qui caractérise sa résistance à la flexion (au prorata du module de Young du matériau), alors :
$$ \large {I(c,e) = \frac{1} {2 \times 3^{2,5}} \times \left[2 (c+e)^4 - \left(\frac{c} {2} -e \right)^4 - \left(\frac {c} {2} + 2e \right) ^4 \right]}$$
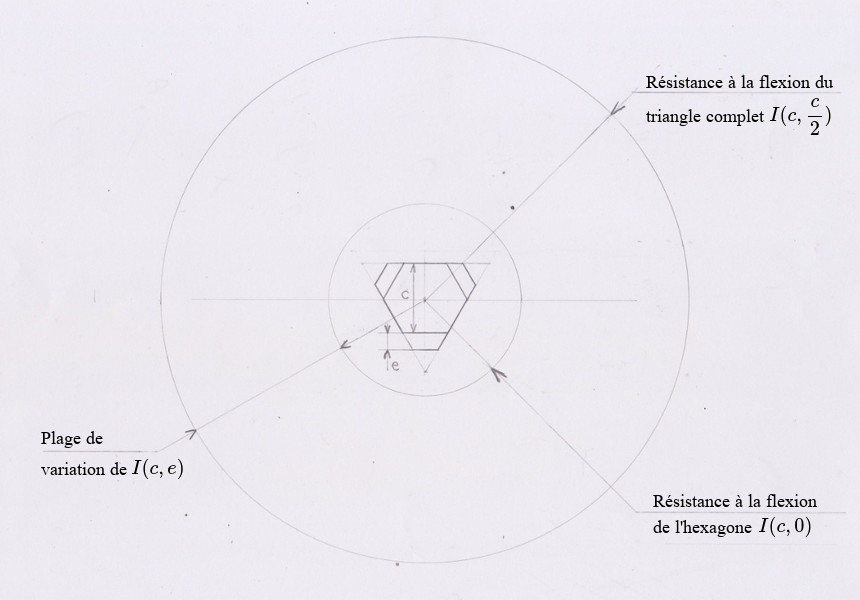
Cette formule, en ayant les données de \(c\), mesurées avant le collage des renforts et de \(e\) après collage et diminution du renfort, permet de comparer la résistance à la flexion, sur toute sa longueur, de la section renforcée avec celle de l’hexagone initial. On peut vérifier que pour \(e=0,\; I(c,0)\) est égal au moment d’inertie de l’hexagone et que pour \(e=\dfrac{c}{2}\), c'est-à-dire si on a conservé le triangle complet, \(I \left(c,\dfrac{c}{2} \right)\) est égal à 2,7 fois celui de l’hexagone.
Le calcul de \(I(c,e)\) n’exige qu’une calculatrice pour le collège.
Je reviens et détaille la procédure que j’ai suivie sur le premier prototype “ M.B.I. ” : Partir d’une canne avec un talon non encore équipé de sa poignée. La peser, mesurer sa fréquence à vide, repérer sa courbe en charge statique, par exemple un newton, et l’essayer ! (pour cela utiliser une poignée de fortune, par exemple une tresse épaisse enroulée sur la canne).
Ensuite coller les renforts sur le talon. Il est préférable que les trois baguettes soient exemptes de nœuds, ce qui limite plus ou moins la longueur de la zone renforcée. Sur “ M.B.I. ” elle mesure 40 cm mais je regrette de ne pas l’avoir portée à 55 cm pour avoir un champ de réglage plus vaste. En particulier, j’aurai pu tester une “ Bourrasque ” de 2,15 m ! Une fois les renforts collés, on constate une raideur énorme. Mesurer de nouveau la fréquence à vide.
Avant les premiers lancers, il faut ébaucher des biseaux aux bouts des baguettes de renfort pour qu’elles ne s’arrêtent pas brutalement, puis réinstaller une poignée temporaire.
Comment mettre au point leur profil final ?
Le premier critère c’est l’agrément ressenti à l’usage, qui dépend forcément du lanceur, donc c’est bien de ne pas se limiter à un avis unique ; également le déploiement de la soie qui doit être “ en ligne ” : s’il y a des ondulations, des vagues, cela révèle que l’onde de déformation de la canne a rencontré des zones de faiblesses ou d’excès de raideurs ; enfin, la performance en distance et déterminante. D’essais en essais, on diminue l’épaisseur des renforts en respectant leur égalité sur les trois côtés pour garder l’homogénéité de la résistance à la flexion (pas de points durs). Il ne faut pas arrondir les angles car, en maintenant des plats, on peut mesurer les cotes \(c+e\) . Grâce à ces cotes repérées tout du long du renfort, il sera possible grâce à l’expression de \(I(c,e)\) ci-dessus, de calculer le moment d’inertie de la section et les épaisseurs d’une section hexagonale qui aurait la même évolution des raideurs, l’idée étant de revenir in fine à un hexagone.
C’est une méthode totalement souple : on peut même tout ôter ! Et si on estime en avoir trop ôté, sur le méplat qui reste, on peut recoller un triangle : c’est réversible ! On a bien un talon réglable !
C’est une méthode expérimentale, à défaut d’un programme de calcul. Cela me fait penser au dégradé sur les biseaux d’un assemblage en épissure qui se fait « au toucher », jusqu’à ce que la raideur de l’assemblage soit la même dans toutes les directions de flexion.
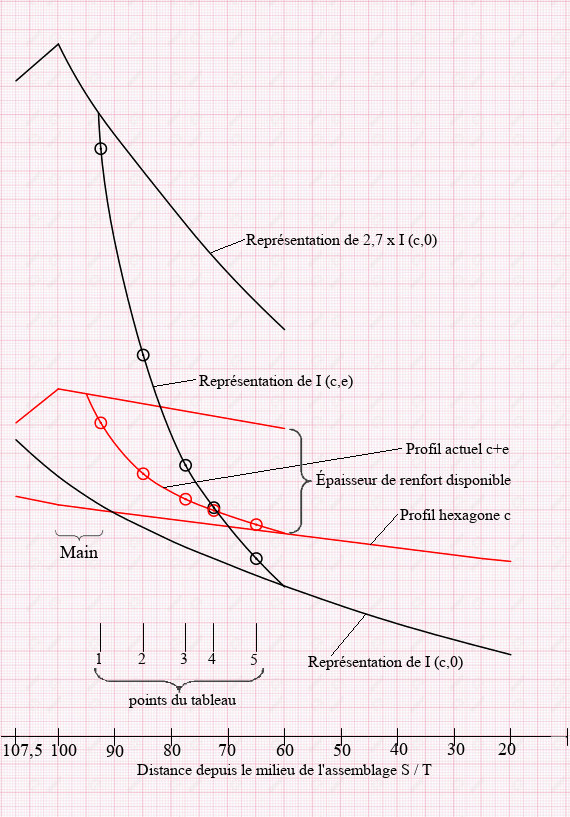
Pour les graphiques, j’ai utilisé le système de représentation des moments d’inertie ou quadratiques que j’ai expliqué dans le paragraphe « Études de profils de cannes » (voir \(C⁴/500\)).
Les valeurs de \(c\) et \(c+e\) sont représentées en rouge (épaisseurs de l’hexagone et du renfort). Les moments d’inertie ou quadratiques sont en bleu. La variation de \(e\) va donner une courbe entre les deux tracés en rouge \(c\) et \(c+ \large \frac{c} {2}\) à laquelle va correspondre une courbe des moments d’inertie \(I (c,e)\) entre les deux tracés en bleu, \(I (c,0)\) hexagone nu et \(2,7 \times I(c,0)\) hexagone avec triangles complets.
Sur “ M.B.I. ” j’ai décidé d’une \( \underline {\text{$1^{re}$ courbe des valeurs de } I (c,e)}\) qui se raccorde avec celle de l’hexagone initial qu’on peut noter \(I (c,o)\) et j’en ai déduit les valeurs de \(e\).
Les valeurs de \(c\) et \(e\) se lisent sur le graphique. Pour calculer \(I (c,e)\) mettre en mémoire \(K_1= \large \frac{1}{2 \times 3^{3,5}}\)
| Position en cm | 92,5 | 85 | 77,5 | 72,5 | 65 |
| \(c\) mm | 8,00 | 7,8 | 7,6 | 7,5 | 7,3 |
| \(e\) mm | 3,1 | 1,5 | 0,8 | 0,5 | 0,2 |
| \(c + e\) | 11,1 | 9,3 | 8,4 | 8 | 7,5 |
| \( {\large\frac{c} {2}} -e\) | 0,9 | 2,4 | 3 | 3,25 | 3,45 |
| \( {\large \frac {c} {2}} + 2e\) | 10,2 | 6,9 | 5,4 | 4,75 | 4,05 |
| \(I(c,e)\) mm⁴ | 626,63 | 406,10 | 289,51 | 242,85 | 189,80 |
| \(I(c,e) \times K_2\) cm | 20,8 | 13,5 | 9,6 | 8,1 | 6,3 |
Pour tracer \(I (c,e)\) en respectant l’échelle déjà utilisée, il faut multiplier \(I (c,e)\) par \(K_2=\large \frac{144}{5 \sqrt3 \times 500}\), un 2e coefficient à mettre en mémoire.
Les essais sont concluants, beau développement de la soie sans ondulation, tenue facile d’une bonne longueur d’une DT 5. Sur le schéma j’ai indiqué un deuxième profil des renforts à tester.
La réponse est donnée par un exemple :
Talon nu avec cote à la base \(C_0\) = 8 mm et \(C_50\) =7 mm pente 0,2 %
Renforts collés sur 50 cm. La hauteur des sections des baguettes de renfort est 4 mm à la base et 3,5 mm à 50 cm de la base (la moitié des valeurs de \(C\)). On suppose qu’on diminue linéairement la hauteur des renforts, de 4 mm à zéro (moins 0,8 mm tous les 10 cm).
Voir tableau ci-dessous et schéma
| Position cm | 0 | 10 | 20 | 30 | 40 | 50 |
| \(C\) mm | 8 | 7,8 | 7,6 | 7,4 | 7,2 | 7 |
| \(C^4/500\) | 8,19 | 7,4 | 6,67 | 6,00 | 5,37 | 4,80 |
| \(e\) mm | 4 | 3,2 | 2,4 | 1,6 | 0,8 | 0 |
| \(C+e\) mm | 12 | 11 | 10 | 9 | 8 | 7 |
| \(C/2-e\) mm | 0 | 0,7 | 1,4 | 2,1 | 2,8 | 3,5 |
| \(C/2+2e\) mm | 12 | 10,3 | 8,6 | 6,9 | 5,2 | 3,5 |
| \(I(C,e)\) mm⁴ | 655 | 578,2 | 466 | 347,6 | 273,3 | 144,4 |
| Représentation cm | 22,1 | 19,2 | 15,5 | 11,55 | 7,89 | 4,80 |
Les lignes 5, 6, 7 donnent les valeurs permettant de calculer \(I (C;e)\)
Ligne 5 : \(C+e\)Ligne 6 : \(C/2-e\)Ligne 7 : \(C/2+2e\)
Sur le schéma j’ai représenté les moments quadratiques de l’hexagone nu par la courbe \(C^4/500\) et j’ai divisé \(I (C,e)\) par \(\dfrac{500 \times 5\sqrt{3}}{144}\) pour respecter les proportions.
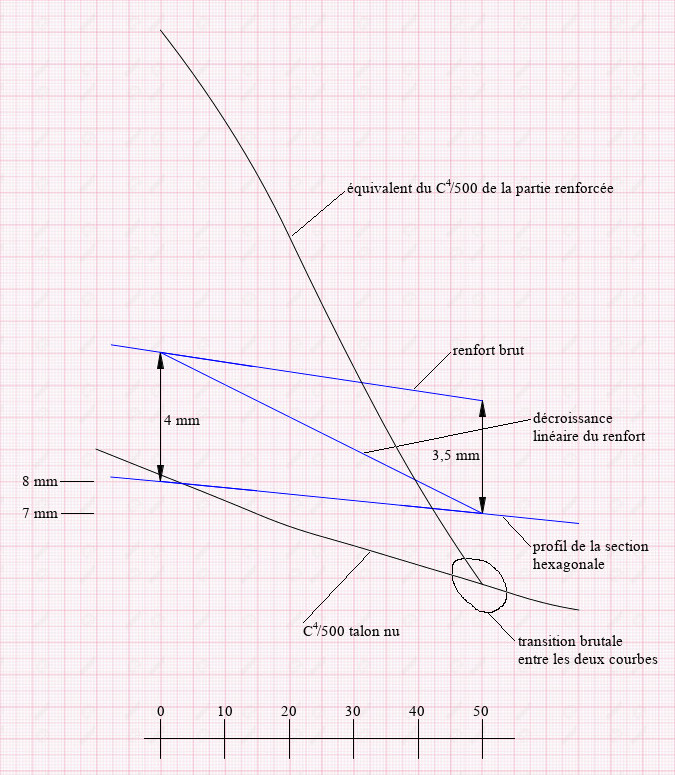
On constate le mauvais raccordement de la résistance à la flexion de la partie renforcée sur la suite du talon, avec même une cause de rupture au point d’arrêt du renfort.
En conclusion, si la formule de calcul de \(I (C,e)\) ne renseigne pas sur le choix du profil des renforts elle permet d’éliminer les fausses “ bonnes solutions ”.
Dans l’attente d’une période plus favorable à des essais partagés !
22 avril 2020

E. GARRISSON dans le courant des années 30 aurait pu reprendre à son compte « du passé faisons table rase » concernant la conception des cannes à mouche. Il a bousculé la tradition qui régnait chez les manufacturiers en Grande-Bretagne ou en France, ou chez les multiples artisans aux États-Unis. Tradition, il faut bien le dire, qui n’a pas engendré l’équivalent des Stradivarius. Quelle canne à mouche, à matériau égal, antérieure à 1980 est capable de rivaliser avec les productions actuelles ? Il faut donc lui savoir gré de sa remise en cause des conicités empiriques et d’avoir été le premier à proposer un moyen de calculer en chaque point de la canne son épaisseur (cote sur plats \(C\)) en fonction de ce qui la plie, le moment de flexion \(M\) en ce point qui cumule ceux dus à la propulsion de la ligne, du bambou, des viroles, des anneaux et jusqu’au vernis situés en amont de ce point, en rapport avec les propriétés élastiques du matériau.
Ses recherches ont abouti à la relation suivante entre \(M\) et \(C\) :
\(C=\sqrt[3]{M/0,120 f}\)
\(f\) étant la contrainte admise en onces par pouces au carré. Dans le système universel SI reconnu par tous les pays, sauf les États-Unis, le Liberia et la Birmanie, l’unité est le Pascal en Newton par mètres carrés \(N.m^{-2}\) qui est une unité de pression. Le coefficient 0,120 résulte du choix des unités.
Cette relation peut se lire ainsi : « \(C\) est égale à la racine cubique du moment de flexion divisé par 0,120 fois la contrainte \(f\) admise. »
Et comme elle s’applique en chaque point de la canne repéré par sa position \(x\) il est légitime de faire apparaître cet indice \(x\) :
\(C_x=\sqrt[3]{M/0,120 f}\)
La parenté avec la condition d’égale contrainte qui figure dans le chapitre « Résultats théoriques » est évidente :
| L’égale contrainte impose que le rayon \(r\) de la tige soit proportionnel en tout point à la racine cubique du moment fléchissant. |
(Exemple : si \(MtF\) est multiplié par 8, le rayon \(r\) doit être doublé : \( \sqrt[3]{8} =2 \) )
Ce qui revient à écrire, si la cote sur plats est \(C_x\) et le moment fléchissant \(M_x\)
\(C_x=k.\sqrt[3]{Mx}\)
Dans ma méthode, le coefficient \(k\) est défini par le choix de \(C_0\), la cote sur plats “ sous la main ”, et le moment en ce point \(M_0\) qui cumule ceux nécessaires à la propulsion de la ligne et de toute la canne. On a donc \(k= C_0 \text{/} \sqrt[3]{M_0}\)
E. GARRISSON aurait-il sans le dire calculé des profils d’égale contrainte ? La vérité est plus complexe.
Cela tient à sa méthode de calcul des moments fléchissants. Un moment est le produit d’une distance par une force (il est plus précis de le définir comme produit vectoriel d’un vecteur “ bras de levier ”, \(\overrightarrow{OM}\)par un vecteur \(\overrightarrow{F}\) associé à la force qui s’applique en \(M\)).
Pour la force, E. GARRISSON, au lieu d’utiliser la relation \(F= M.\gamma\), \(\gamma\) étant l’accélération que l’on communique soit à la ligne soit à un élément précis de la canne, qui est donc une grandeur variable, utilise un “ impact factor ” d’une valeur constante égale à 4. Il en a donné une définition « terme défini en langage d'ingénieur comme le rapport de la déformation dynamique maximum à la déformation statique ». Ce qui m’a renforcé dans mon idée de le considérer comme une accélération constante de tous les points de la canne qui serait égale à 4G, G étant l'accélération de la pesanteur terrestre ?
Sous réserve d’une erreur de ma part, ce serait la négation totale de ce qu’est une canne à mouche dont le seul rôle est de communiquer en pointe du scion, grâce à son bras de levier et sa détente, une accélération que l’on n’est pas capable de donner avec notre seule main dans la poignée ! Autrement dit : E. GARRISSON modéliserait le mouvement de la canne comme une translation sans rotation !
La conséquence de cet impact factor constant est de surévaluer les moments pour la propulsion du talon, au détriment de celui pour propulser la ligne et conduit à un affaiblissement des scions. E. GARRISSON, resté prisonnier de son impact factor de 4 (est-ce dû à son expérience professionnelle ?), alors qu’il aurait dû le faire croître du talon au scion par une méthode de son choix, a choisi pour retravailler ses profils de modifier le facteur \(f\), qu’il appelle contrainte mais qui n’en est pas une du fait de l’irréalité complète de ses moments fléchissants. D’où ses courbes de contraintes qui sont, d’après mon hypothèse précédente, complètement fictives et permettent finalement d’obtenir le profil que l’on veut.
Je suis conscient du coté iconoclaste de mes propos et j’espère grâce à leur publication démêler le vrai du faux.
En attendant, je reste perplexe devant la “ statue du Commandeur ” érigée par ses disciples qui, 90 ans après sa mise au point, continuent d’utiliser sa méthode, de présenter des pseudos courbes de contraintes et d’en discuter doctement alors que, pour ma part, ses travaux ne sont qu’une étape dans le mouvement perpétuel de l’évolution des recherches.
E. GARRISSON a le mérite, comme déjà dit en introduction, de s’être émancipé de l’empirisme, d’avoir eu l’idée de calculer un profil en tenant compte de la propulsion de la canne et pas seulement de celle de la ligne. D’avoir prôné un renfort de conicité en sortie de poignée. D’avoir débarrassé la canne de tout ce qui l’enjolive sans l’améliorer, une approche minimaliste que je partage... Il reste à mes yeux un visionnaire. J’ajoute que ses méthodes auraient probablement évolué s’il avait disposé de moyens de calculs plus puissants.
05 septembre 2021
