LES CANNES À MOUCHE de DANIEL BRÉMOND
| Accueil | Genèse | Structure alvéolaire | Assemblage par épissures | Études de profils | Résultats théoriques | Souvenirs | Contact |

| Accueil | Genèse | Structure alvéolaire | Assemblage par épissures | Études de profils | Résultats théoriques | Souvenirs | Contact |
Mon apport à la technique d’assemblage en biseau par épissures, en sifflet pour Josselin de LESPINAY, ″spliced″ pour les anglais. Date : 1976



Au départ, c’est une méthode d’assemblage ancestrale, qui fait penser à une greffe.

Au titre des inconvénients :

Mais, en contrepartie, que de qualités !
La naissance d’un premier “ spliced ” moderne !
Un ami, Yves RAMEAUX, à la fois très grand pêcheur et très grand collectionneur, m’avait demandé de lui construire une canne, la plus sobre possible, donc justement avec un assemblage par épissure. Il m’avait confié comme modèle une Sharpe « Split Cane Fly Rod » en bambou imprégné. (Je n’ai jamais eu d’information sur cette imprégnation qui, à posteriori, m’a semblé très bien adaptée aux biseaux qui ne seraient pas suffisamment protégés par un vernis traditionnel). Son souhait était de conserver le profil hexagonal dans la zone d’assemblage, sans aucun renfort.
Au premier essai du prototype j’ai constaté un affaiblissement considérable de la résistance à la flexion dans le plan vertical (l’axe de la déformation et la fibre neutre sont horizontaux). Des calculs m’ont permis de vérifier qu’au milieu des biseaux, là où l’hexagone est partagé en deux, elle ne représentait plus que \(\dfrac{13}{45}\) de la section d’origine, soit à peine plus du quart. (Voir schéma des différentes résistances à la flexion, tracés en bleu et vert).
En bleu, la résistance à la flexion d'un hexagone plein.
En vert, la résistance à la flexion de l'hexagone fendu horizontalement.
En rouge, la résistance à la flexion de l'hexagone fendu, complété des deux triangles équilatéraux sommitaux collés.
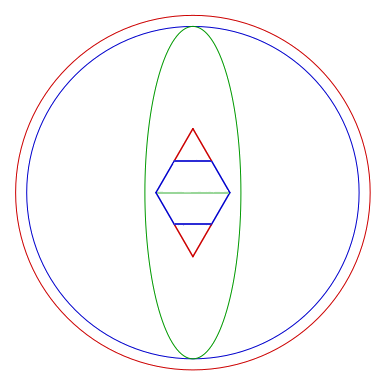
Comment y remédier ? Certainement pas en gonflant la section dans tous les sens parce que le partage en deux de la section conserve la résistance à la flexion dans le sens transversal. Il n’y avait la nécessité de rattraper la résistance à la flexion que dans le plan vertical.
Comment y parvenir ? J’ai eu l’idée de compléter les demi-hexagones par des baguettes triangulaires, collées sur leur petite base, possibilité qui demandait à être validée par le calcul. Et là, très bonne surprise : j’ai constaté qu’on pouvait, de cette façon, rattraper l’affaiblissement causé par le partage en deux de la section ! La résistance à la flexion des deux demi-hexagones devenus, du fait du renfort, des triangles équilatéraux, représente, dans toutes les directions de flexion, exactement les \(\dfrac{16}{15}\) de l’hexagone complet (tracé en rouge) ! Juste ce qu’il faut pour être sûr de pouvoir compenser l’affaiblissement lié au partage en deux ! (Le bambou n’est pas homogène, les fibres sont plus serrées vers la face extérieure, celle qui est collée, et moins denses au sommet du triangle).
Mais que se passe-t-il quand on s’éloigne du milieu de l’assemblage, quand l’hexagone initial est partagé en deux parties inégales ? Par exemple ¾ et ¼ de la cote sur plats. Dans ce cas il suffit d’un renfort moins haut : on ne complète pas par un triangle mais par un demi-trapèze. D’où la forme en losange très effilé des biseaux accolés (voir les illustrations de l'article « de A à Z »).
Il est possible mais un peu laborieux de calculer les épaisseurs des renforts pour, tout du long des biseaux accolés, compenser leur partage en deux, aussi j’ai préféré réaliser cette juste compensation expérimentalement. Pour cela il faut assembler les biseaux par un ruban adhésif, les mettre en flexion et imposer une rotation à l’ensemble. Tant que l’on ressent une raideur plus forte dans le plan vertical, il faut amincir le renfort, symétriquement par rapport au point médian, sachant qu’à cet endroit il faut se garder de diminuer la hauteur des baguettes de renfort et se limiter à arrondir l’angle vif. On répète les essais jusqu’à ce que la résistance à la flexion soit la même dans toutes les directions. C’est l’affaire de moins d’une heure de mise au point pour que les biseaux assemblés se comportent exactement comme une section hexagonale complète !
Cet ajustement réalisé, il est indispensable de protéger les deux zones d’assemblage par une résine époxy, chauffée pour qu’elle imprègne bien les fibres du bambou, en couche très mince étendue au doigt.
J’ai baptisé “ Lacédémone ” cette première canne “ spliced ” avec des biseaux calculés et non approximatifs, un nom choisi pour évoquer la sobriété du procédé.
Je précise que j’ai toujours usiné les faces d’assemblage à main levée, sans aucun guidage, de même l’ “ effilement ” des renforts, avec mes outils habituels, tranchet, lime d’affûtage, et pied à coulisse pour vérifier avec sa règle la planéité des biseaux.

Après “ Lacédémone ”, j’ai pratiquement abandonné l’utilisation de viroles et, depuis ce premier modèle, aucune de mes cannes n’a présenté de faiblesse au niveau de l’épissure.
Un détail amusant : quand on commence à enrouler le ruban perpendiculairement à la canne, la conicité de l’assemblage fait qu’il se place de lui-même en hélice puis se retrouve perpendiculaire quand on arrive à l’autre bout. De quoi nous couper le sifflet !
Des conseils (le 4e est d'une portée générale) :
Décalage du milieu de la section hexagonale par rapport au milieu du biseau du fait de la conicité
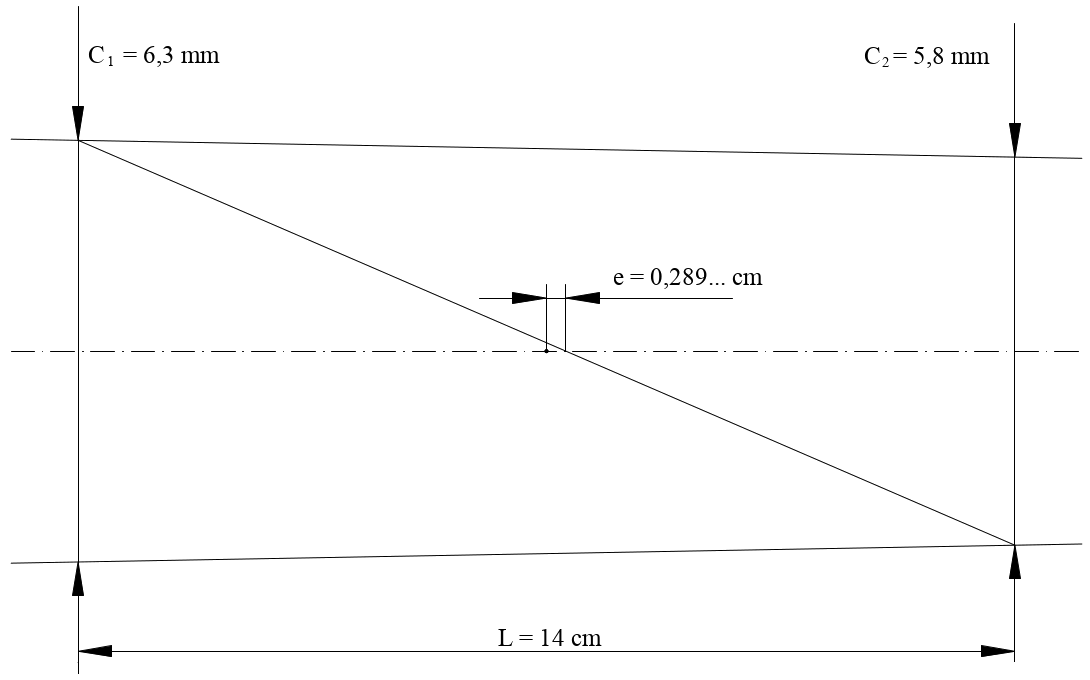
\(e=\displaystyle \frac{L\times C_1}{C_1+C_2}-\frac{L}{2}\) \(e= \displaystyle \frac {14 \times \textcolor{red}{6,3}}{\textcolor{red}{6,3 + 5,8}} - \frac {14}{2} = 0,289\;\text{cm} \approx 3\;\text{mm}\)

